TU Wien:Mathematik 1 VO (Panholzer)/Stoff WS05/9. VO 03.11.2005

Relationen (Fortsetzung)

ÄR: (R),(S),(T)

Eine Menge (System) von Teilmengen $\{K_{i}:i\in I\}$ von der Menge A heißt Klasseneinteilung (=Partition), falls folgende Bedingungen erfüllt sind:

1. $K_{i}\neq 0,\forall i\in I$
2. $K_{i}\cap K_{j}=0,i\neq j,i,j\in I$
3. $\bigcup K_{i}=A,i\in I$

Beispiel: A = {1,2,3,4,5}

Relation: ${\text{a R b }}:\Leftrightarrow a\equiv b{\text{ mod 3 }}$

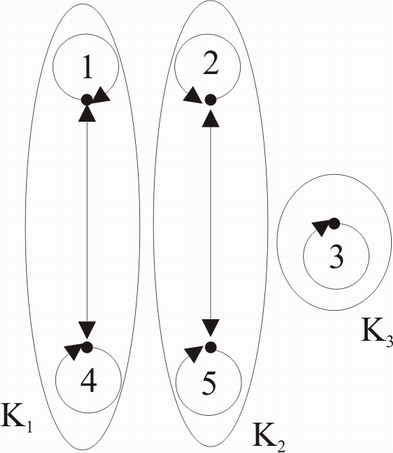
Satz: Die Klasseneinteilungen von A und die ÄR auf A entspechen einander umkehrbar eindeutig.

Sei $\{K_{i}:i\in I\}$ eine Klasseneinteilung von A so entspricht die ÄR Rm definiert durch ${\text{a R b }}:\Leftrightarrow \exists i\in I:ia\in K_{i}\cap b\in K_{i}$ .

(R): a geg.: $\exists i:a\in K_{i}\neq a\in K_{i}\wedge a_{\in }K_{i}=aRa$

(S): a,b geg. a R b; $\exists i:a\in K_{i}\wedge b\in K_{i}\neq bRa$

(T): a,b geg. sodass ${\text{a R b }}\wedge {\text{b R c }}$, d.h. $\exists i:a\in K_{i}\wedge b\in K_{i}$ und $\exists j:b\in K_{j}\wedge c\in K_{j}$

$\Rightarrow b\in K_{i}\wedge b\in K_{j}\Rightarrow b\in K_{i}\cap K_{j}$

$\Rightarrow K_{i}=K_{j}\Rightarrow a\in K_{i}\wedge c\in K_{i}\Rightarrow aRc$

Sei R eine ÄR auf A, so entspricht dieser der Klasseneinteilung $\{K(a):a\in A\}$, definiert durch: $K(A);=\{b\in A:bRa\}$.

Weiters gilt: $aRb\Leftrightarrow K(a)=K(b)$

1. K(a) = 0, weil $a\in K(a)$ und a R a
2. K(a) $\cap$ K(b) $\neq 0\Rightarrow K(a)=K(b)$

K(a) $\cap K(b)\neq 0\Rightarrow \exists c\in A:c\in K(a)\wedge c\in K(b)$

$\Rightarrow cRa\wedge cRb\Rightarrow bRc\wedge cRa$

$\Rightarrow bR\Rightarrow {\text{ Def. }}K(a)=K(b)$

1. $\cup K(a)\subseteq \cup \{a\}=a\qquad a\in A$ und $\cup K(a)\subseteq A$ ergeben $\cup K(a)=A$

$aRb\Leftrightarrow b\in K(a)\Leftrightarrow K(a)=K(b)$

Beispiel: Restklassenzerlegung ${\text{ mod 4 }}$

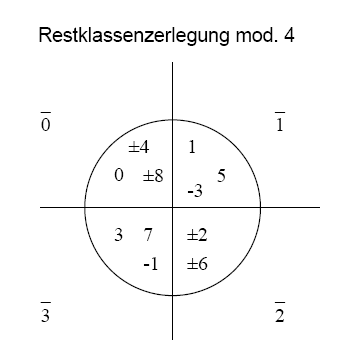
(Herzlichen Dank an Johannes Matiasch! --Mnemetz 19:25, 4. Nov 2005 (CET))

$\mathbb {Z}$, ÄR $\equiv {\text{ mod m }}\Rightarrow$ Klasseneinteilung {${\overline {0}},...$} (bis m-1)

Geg. ÄR R, Menge aller Klassen von A zerlegt nach R nennt man Faktormenge "A/R" (A modulo R).

Beispiel: Allrelation $\alpha =A^{2}$

A / $\alpha$

• Identische Relation: $\epsilon =\{(a,a),a\in A\}$

A / $\epsilon =\{\{a\}:a\in A\}$

Halbordnungsrelation: (R),(A),(T)

• $a<b\qquad \Leftrightarrow \qquad a\leq b\wedge a\neq b$
• $a\geq b\qquad \Leftrightarrow \qquad b\leq a$
• $a>b\qquad \Leftrightarrow \qquad b\leq a\wedge a\neq b$

$\leq$ Halbordungsrelation auf A: Dann gilt

• g grösstes Element: $\Leftrightarrow g\geq x,\forall x\in a$
• k kleinstes Element: $\Leftrightarrow k\leq x,\forall x\in a$
• M maximales Element: $\Leftrightarrow$ es existiert kein $x\in A:x>M$
• m minimales Element: $\Leftrightarrow$ es existiert kein $x\in A:x<m$

$\geq$ Halbordungsrelation auf A: Paar $\langle A,\leq \rangle$ heißt halbgeordnete Menge (Halbordnung)

Beispiel: $\langle \mathbb {N} ,\leq \rangle$ natürliche Ordnung;

• $\nexists g$
• $k=0$
• $\nexists M$
• $m=0$

Beispiel: $\langle \mathbb {R} ,\leq \rangle$

• $\nexists g$
• $\nexists k$
• $\nexists M$
• $\nexists m$

M geg,; $\langle P(M),\subseteq \rangle$

• k = 0 , g = M

M geg,; $\langle P(M)\{0\},\subseteq \rangle$ g = M, $\nexists k$

Alle einelementigen Mengen sind minimale Elemente

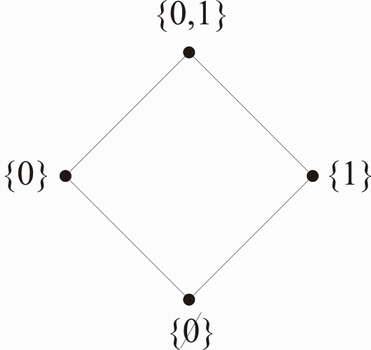
Klassische Darstellung von Halbordnung:

• Graph $G\leq$
• besser mittels Hasse-Diagramm

Definition: $\langle A,\leq \rangle$ gegegben: a bleibt unterer Nachbar von b (bzw. b oberer Nachbar von a) $\Leftrightarrow$ es existiert kein $c\in A:a>c>b\Rightarrow$ Nachbarschaftsrelation

Darstellung des Graphen der Nachbarschaftsrelation.

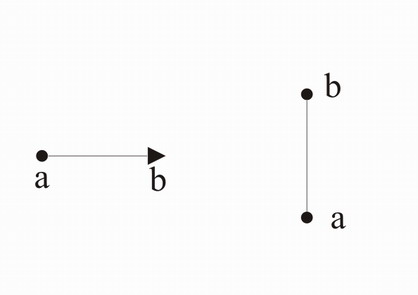
Bsp.: M={0,1}, $\langle P(M)\setminus \{\varnothing \},\subseteq \rangle$