TU Wien:Analysis 2 UE (diverse)/Übungen SS23/Beispiel 79
Zur Navigation springen
Zur Suche springen
sei der durch , und berandete beschränkte Bereich der -Ebene. Man berechne
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Theoretische Grundlagen: Gebietsintegral[Bearbeiten | Quelltext bearbeiten]
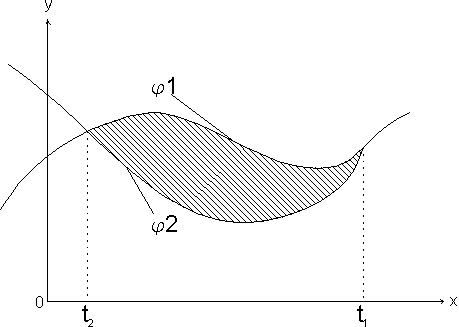
Zwei Funktionen und , welche ein Gebiet begrenzen ( "oben", "unten") sind die Grenzen für die zu berechnende Fläche. Diese Funktionen seien explizit in der Form gegeben.
Die niedrigere "x-Grenze" des Flächenstücks sei durch gegeben, die höhere durch .
Nun gilt für das Gebietsintegral folgende Formel:
Lösungvorschlag[Bearbeiten | Quelltext bearbeiten]
Lösungsvorschlag von mxr[Bearbeiten | Quelltext bearbeiten]
SS08 falls Link nicht geht, dann
SS08 Beispiel 157
Lösung aus Karigl 2004[Bearbeiten | Quelltext bearbeiten]
- PDF aus Karigl 2004 --Markus Nemetz 11:29, 10. Mai 2006 (CEST)
Informatikforum[Bearbeiten | Quelltext bearbeiten]
- Beispiel 61 (MA2) --Markus Nemetz 08:29, 16. Mai 2006 (CEST)
- UE Runde 8 (18.05.06), Gruppe 12, Allg. Tipps --Markus Nemetz 11:29, 10. Mai 2006 (CEST)
- Diskussion Informatik-Forum WS08 Beispiel 33 Karigl