TU Wien:Mathematik 2 UE (diverse)/Übungen WS10/Beispiel 13
Zur Navigation springen
Zur Suche springen
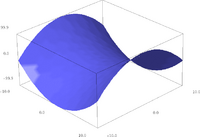
3D Plot von 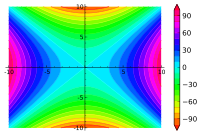
Höhenlinien von 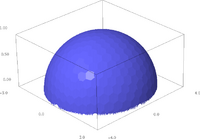
3D Plot von 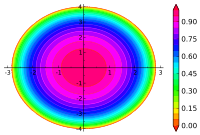
Höhenlinien von
Man stelle den Definitionsbereich und den Wertebereich folgender Funktionen fest und beschreibe die Höhenlinien:
(a)
(b)
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
Beispiel (a)[Bearbeiten | Quelltext bearbeiten]


Definitionsbereich:
Wertebereich:
Höhenlinien:
Beispiel (b)[Bearbeiten | Quelltext bearbeiten]


Definitionsbereich:
Daraus folgt:
Wertebereich: , da der Wert unter der Wurzel nur zwischen 0 und 1 sein kann.
Höhenlinien:
kann man zu zusammenfassen, da es konstant ist. Da Werte zwischen 0 und 1 annehmen kann ist der Wertebreich für c 0 () bis 16 ().
Links[Bearbeiten | Quelltext bearbeiten]
- TU Wien:Mathematik 2 UE (diverse)/Übungen SS06/Funktionen in mehreren Variablen 1 (ähnliches Beispiel)