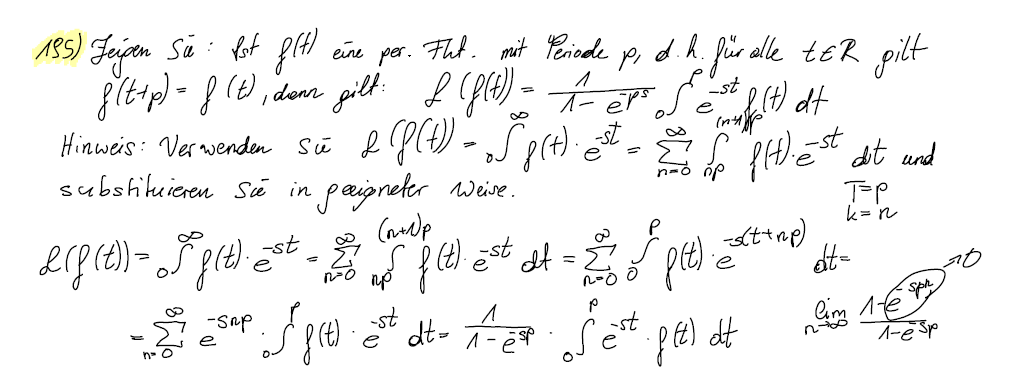TU Wien:Analysis 2 UE (diverse)/Übungen SS23/Beispiel 227
(Weitergeleitet von TU Wien:Mathematik 3 UE (diverse)/Übungen WS06/Beispiel 39)
Man zeige: Ist f(t) periodisch mit Periode p, d. h. f(t + p) = f(t) für alle t, dann gilt
Anmerkung: Man verwende und substituiere geeignet.
Dieses Beispiel ist als Datei markiert. Ist dies falsch oder ungenau? Aktualisiere den Lösungsstatus (Details: Vorlage:Beispiel)
Lösung[Bearbeiten | Quelltext bearbeiten]
Hilfreiches[Bearbeiten | Quelltext bearbeiten]
Websites[Bearbeiten | Quelltext bearbeiten]
- Thread im Informatik-Forum --Markus Nemetz 13:29, 23. Nov 2006 (CET)
- Beispiel E --Markus Nemetz 13:29, 23. Nov 2006 (CET)