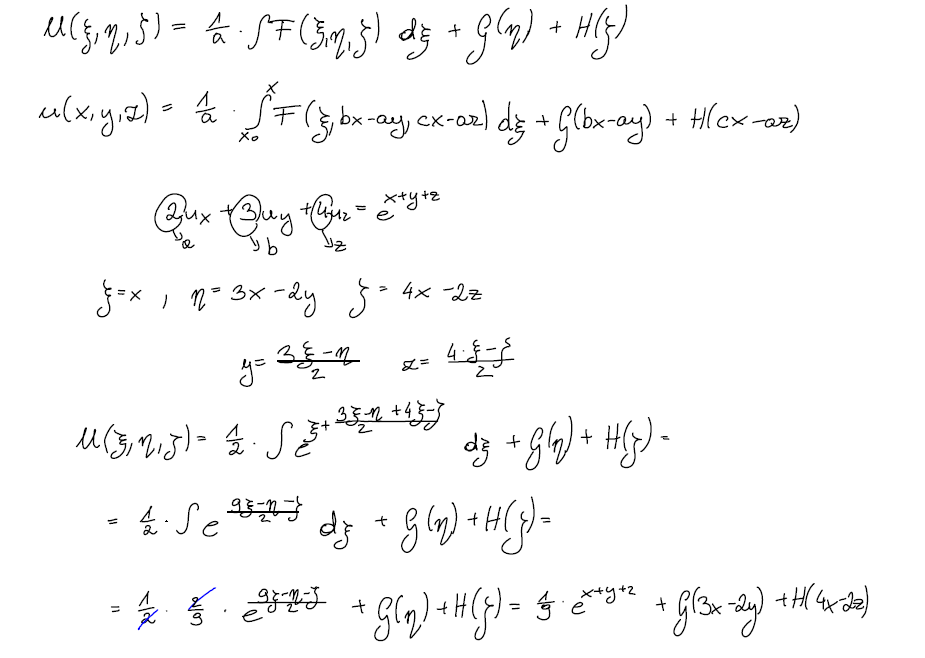TU Wien:Analysis 2 UE (diverse)/Übungen SS23/Beispiel 357

Man betrachte die lineare partielle Differentialgleichung erster Ordnung mit konstanten Koeffizienten in drei Variablen

$a{u}_x+b{u}_y+c{u}_z=f(x,y,z)(a,b,c\in ℝ)$.

Man zeige, dass diese Gleichung mit Hilfe der Substitution

$\xi =x$, $\eta =bx-ay$, $\zeta =cx-az$

allgemein gelöst werden kann. Insbesondere finde man damit die allgemeine Lösung der Gleichung

$2u_x+3u_y+4u_z=e^{x+y+z}$.

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Lösungsvorschlag

$x=\xi$

$y=\frac{bx-\eta }{a}$

$z=\frac{cx-\zeta }{b}$

$U(\xi ,\eta ,\zeta )=u(\xi ,\frac{bx-\eta }{a},\frac{cx-\zeta }{b})=u(x,y,z)$

$F(\xi ,\eta ,\zeta )=f(\xi ,\frac{bx-\eta }{a},\frac{cx-\zeta }{b})=f(x,y,z)$

$\begin{array}{cc}F(\xi ,\eta ,\zeta )& =f(x,y,z)\\ & =a{u}_x+b{u}_y+c{u}_z\\ & =a(U_{\xi }{\xi }_x+U_{\eta }{\eta }_x+U_{\zeta }{\zeta }_x)+b(U_{\xi }{\xi }_y+U_{\eta }{\eta }_y+U_{\zeta }{\zeta }_y)+c(U_{\xi }{\xi }_z+U_{\eta }{\eta }_z+U_{\zeta }{\zeta }_z)\\ & =a(1\cdot U_{\xi }+b\cdot U_{\eta }+c\cdot U_{\zeta })+b(0\cdot U_{\xi }-a\cdot U_{\eta }+0\cdot U_{\zeta })+c(0\cdot U_{\xi }+0\cdot U_{\eta }-a\cdot U_{\zeta })\\ & =a{U}_{\xi }+ab{U}_{\eta }+ac{U}_{\zeta }-ab{U}_{\eta }-ac{U}_{\zeta }\\ & =a{U}_{\xi }\end{array}$

$\begin{array}{cc}U(\xi ,\eta ,\zeta )& =\frac{1}{a}\int F(\xi ,\eta ,\zeta )\mathrm{d}\xi +G(\eta )+H(\zeta )\\ u(x,y,z)& =\frac{1}{a}{\int }_{x_0}^{x}F(\xi ,bx-ay,cx-az)\mathrm{d}\xi +G(bx-ay)+H(cx-az)\end{array}$

In der Gleichung $2u_x+3u_y+4u_z=e^{x+y+z}$ sind $a=2$, $b=3$, $c=4$ und $f(x,y,z)=e^{x+y+z}$. Daraus folgen $\xi =x$, $\eta =3x-2y$, $\zeta =4x-2z$, $y=\frac{3\xi -\eta }{2}$ und $z=\frac{4\xi -\zeta }{2}$.

$\begin{array}{cc}U(\xi ,\eta ,\zeta )& =\frac{1}{2}\int e^{\xi +\frac{3\xi -\eta }{2}+\frac{4\xi -\zeta }{2}}\mathrm{d}\xi +G(\eta )+H(\zeta )\\ & =\frac{1}{2}\int e^{\frac{9\xi -\eta -\zeta }{2}}\mathrm{d}\xi +G(\eta )+H(\zeta )\\ & =\frac{1}{2}\cdot \frac{2}{9}{e}^{\frac{9\xi -\eta -\zeta }{2}}+G(\eta )+H(\zeta )\\ & =\frac{1}{9}{e}^{\frac{9\xi -\eta -\zeta }{2}}+G(\eta )+H(\zeta )\\ u(x,y,z)& =\frac{1}{9}{e}^{\frac{9x-3x+2y-4x+2z}{2}}+G(3x-2y)+H(4x-2z)\\ & =\frac{1}{9}{e}^{x+y+z}+G(3x-2y)+H(4x-2z)\\ \end{array}$

Lösungsvorschlag

Links

• Älterer Thread im Informatik-Forum, entspr. dort Bsp. 78

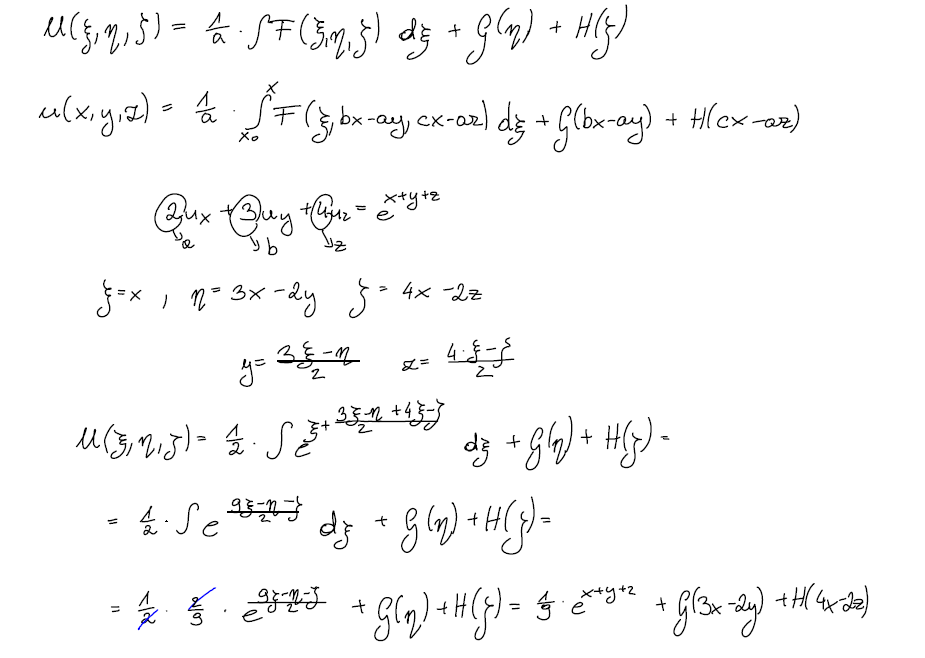
Anmerkungen:

Da nur 1x integriert wird, kommen nicht zwei (G und H), sondern nur eine Funktion dazu, die von Eta und Zeta abhängt.