TU Wien:Statistik und Wahrscheinlichkeitstheorie UE (Stadler)/Übungen SS09/Beispiel 16

Bei der Messung des Durchmessers von Lagerbuchsen wurden folgende Abweichungen (in μm) vom Nennmaß 10 mm gemessen:

-13.29, -9.65, -9.58, -9.51, -8.01, -6.78, -6.52, -5.28, -4.98, -3.98, -3.65, -1.82, -1.50, -1.32, -1.24, -1.17, -0.88, -0.76, -0.03, 0.00, 0.00, 0.91, 1.15, 1.76, 2.30, 3.36, 3.77, 5.17, 5.78, 6.53, 7.11, 7.13, 8.39, 9.12, 9.76, 10.25, 10.97, 11.87, 12.36, 13.97, 15.31, 17.29, 19.64, 21.39

Es gilt $\sum _{i=1}^{44}x_{i}=115.34$, $\sum _{i=1}^{44}x_{i}^{2}=3277.873$, $\sum _{i=1}^{44}x_{i}^{3}=32038.95$, $\sum _{i=1}^{44}x_{i}^{4}=3705687.5$

Bestimmen bzw. erstellen Sie:

a) Minimum, Maximum und Spannweite (=Maximum-Minimum),

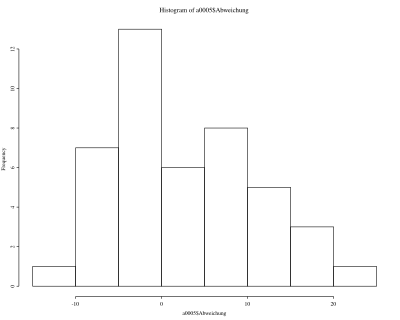
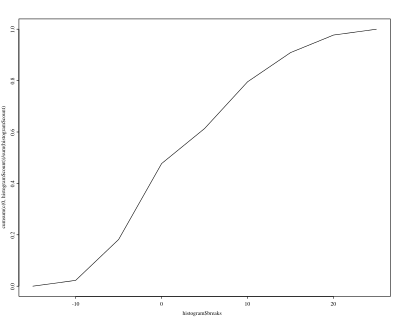
b) zeichnen Sie ein Histogramm und ein Summenhäufigkeitspolygon,

c) den arithmetischen Mittelwert aus den nichtklassierten und aus den klassierten Werten,

d) den Median und den Modalwert.

Lösungsvorschlag

Beispiel (a)

> min(a0005)
[1] -13.29
> max(a0005)
[1] 21.39
> max(a0005) - min(a0005)
[1] 34.68

Beispiel (b)

> hist(a0005$Abweichung)
> plot(histogram$breaks, cumsum(c(0,histogram$count)) / sum(histogram$count), type="l")

Beispiel (c)

> mean(a0005)
Abweichung 
  2.621364
> values <- histogram$breaks[1:(length(histogram$breaks)-1)] + (histogram$breaks[2] - histogram$breaks[1])/2
> sum((values * histogram$count))/sum(histogram$count)  
[1] 2.613636

Beispiel (d)

> median(a0005$Abweichung)
[1] 1.03
> values[which.max(histogram$count)]
[1] -2.5