TU Wien:Statistik und Wahrscheinlichkeitstheorie UE (Stadler)/Übungen SS09/Beispiel 20

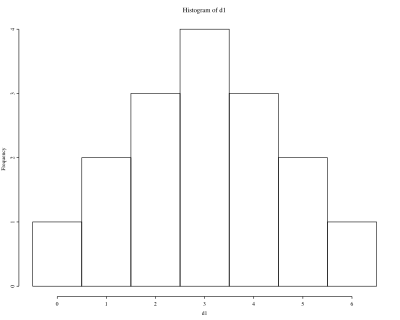
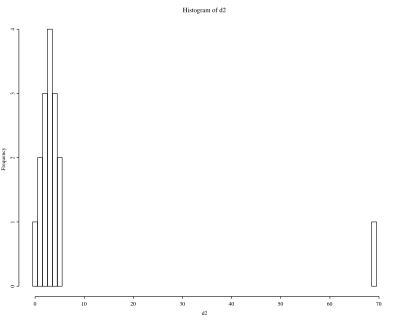
16 Moskauer Frauen seien Ende des vorigen Jahrhunderts nach der Zahl ihrer Kinder befragt worden. Dabei ergab sich die folgende Reihe: 1, 5, 2, 4, 0, 3, 1, 2, 3, 3, 3, 4, 5, 2, 4, 6. Zeichnen Sie ein Histogramm und überprüfen Sie, wie sich folgende Werte ändern, wenn anstelle der oben als letzt genannte Frau (mit 6 Kindern) Fedora Wassilet befragt worden wäre, die seinerzeit 69 Kinder zur Welt brachte und schon mit 56 Jahren starb?

a) arithmetisches Mittel

b) Modalwert

c) Median

d) 10%-gestutztes Mittel

e) Interquartilabstand

f) Spannweite

g) Varianz- und Standardabweichung

h) Schiefe

Wie ändert sich die Kurtosis, wenn anstelle der ersten beiden Frauen, Frauen mit jeweils 3 Kindern befragt worden wären?

Lösungsvorschlag

> d1 <- sort(c(1,5,2,4,0,3,1,2,3,3,3,4,5,2,4,6))
> d2 <- sort(c(1,5,2,4,0,3,1,2,3,3,3,4,5,2,4,69))
> hist(d1, breaks=seq(from=-0.5, to=6.5, by=1))
> hist(d2, breaks=seq(from=-0.5, to=69.5, by=1))

Beispiel (a)

> mean(d1)
[1] 3
> mean(d2)
[1] 6.9375

Beispiel (c)

> (d1[7]+d1[8])/2
[1] 3
> (d2[7]+d2[8])/2
[1] 3

Beispiel (d)

> d1b <- d1[2:15]
> d2b <- d2[2:15]
> mean(d1b)
[1] 3
> mean(d2b)
[1] 3

Alternativ:

> mean(d1, trim=0.1)

Beispiel (e)

> IQR(d1)
[1] 2
> IQR(d2)
[1] 2

Beispiel (f)

> max(d1) - min(d1)
[1] 6
> max(d2) - min(d2)
[1] 69

Beispiel (g)

> var(d1)
[1] 2.666667
> sd(d1)
[1] 1.632993
> var(d2)
[1] 275.9292
> sd(d2)
[1] 16.61112

Beispiel (h)

> library(moments)
> skewness(d1)
[1] 0
> skewness(d2)
[1] 3.239903

Kurtosis

> d3 <- sort(c(3,3,2,4,0,3,1,2,3,3,3,4,5,2,4,6))
> kurtosis(d1)
[1] -0.9609375
> kurtosis(d2)
[1] 9.185127
> kurtosis(d3)
[1] -0.253418