TU Wien:Theoretische Informatik und Logik VU (Gramlich, Oswald)/Prüfung 2011-03-24
Tragen Sie mit Kugelschreiber Kennzahl, Matrikelnummer, Nach- und Vornamen ein. Legen Sie einen Lichtbildausweis bereit. Erlaubte Unterlagen: Skriptum, Vorlesungsfolien; KEINE gelösten Übungsbeispiele. Schreiben Sie alle Lösungen auf diese Blätter und geben Sie die Prüfungsarbeit ohne Zusatzblätter ab. Sie haben 2 Stunden (120 Minuten) zur Bearbeitung der Aufgaben. Viel Erfolg!
Beispiel A/1[Bearbeiten | Quelltext bearbeiten]
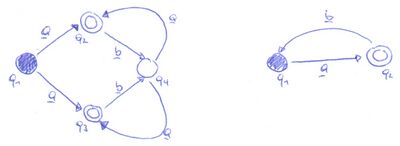
Sei , wobei
a) Geben Sie (also die von akzeptierte Sprache) als reguläre Menge an. (2 Punkte)
b) Gibt es eine kontextfreie Grammatik, welche erzeugt? Falls ja, geben Sie eine solche an. Falls nein, begründen Sie, warum es eine solche nicht geben kann. (4 Punkte)
c) Geben Sie einen deterministischen endlichen Automaten an, welcher das Komplement von akzeptiert. (Graphische Darstellung genügt.) (4 Punkte)
Lösung[Bearbeiten | Quelltext bearbeiten]
a)
b) Eine Grammatik heißt kontextfrei, wenn die linke Seite jeder Produktion ein einzelnes Nonterminalsymbol ist.
mit
Wenn man sich den Automaten aber einmal näher ansieht, wird man feststellen, dass es sich dabei um einen NEA handelt, der aber zu einem DEA vereinfacht werden kann.
Jetzt wird auch deutlich, dass zu dem Automaten auch eine reguläre Grammatik existiert.
mit
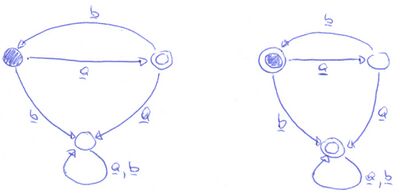
c) Dafür muss lediglich die Falle im DEA von Punkt b) eingebaut werden. Den Automaten, der das Komplement akzeptiert, erhält man dann ganz einfach, indem man alle Endzustände zu Nicht-Endzuständen macht und umgekehrt:
Beispiel A/2[Bearbeiten | Quelltext bearbeiten]
Sei und .
a) Geben Sie kontextfreie Grammatiken so an, dass sowie . (6 Punkte)
b) Geben Sie an. (2 Punkte)
c) Ist eine kontextfreie Sprache? Begründen Sie Ihre Antwort. (2 Punkte)
Lösung[Bearbeiten | Quelltext bearbeiten]
TODO
Beispiel A/3[Bearbeiten | Quelltext bearbeiten]
Geben Sie an, ob die folgenden Aussagen richtig oder falsch sind, und begründen Sie Ihre Antworten. (Zwei Punkte für richtige Antworten mit richtiger Begründung, einen Punkt für richtige Antworten mit leicht mangelhafter Begründung, keinen Punkt für falsche Antworten oder fehlerhafte Begründungen.) (10 Punkte)
| a) | Jede rekursiv aufzählbare Sprache über einem einelementigen Alphabet ist regulär. | ☐ richtig ☒ falsch |
| b) | Für beliebige Sprachen gilt: | ☐ richtig ☒ falsch |
| c) | Das Halteproblem für Turingmaschinen ist unentscheidbar. | ☒ richtig ☐ falsch |
| d) | Es gibt einen Homomorphismus, der die Sprache auf die Sprache | ☐ richtig ☒ falsch |
| e) | Ist , so ist nicht kontextsensitiv. | ☐ richtig ☐ falsch |
Begründung für Punkt a)
TODO
Begründung für Punkt b)
TODO
Begründung für Punkt c)
TODO
Begründung für Punkt d)
TODO
Begründung für Punkt e)
TODO
Beispiel A/4[Bearbeiten | Quelltext bearbeiten]
Gegeben seien die AL-Formeln und . Beweisen Sie mithilfe des Tableau-Kalküls, dass eine logische Konsequenz von und ist, d.h. dass gilt: .
Lösung[Bearbeiten | Quelltext bearbeiten]
gilt genau dann, wenn eine gültige Formel ist.
Nehmen wir an, dass widerlegbar ist, also den Wert f annehmen kann. Lässt sich diese Annahme mithilfe des Tableau Kalküls auf einen Widerspruch führen, so gilt .
| (1) | f: | ||||
|---|---|---|---|---|---|
| (2) | t: | (von 1) | |||
| (3) | f: | (von 1) | |||
| (4) | f: | (von 3) | |||
| (5) | f: | (von 3) | |||
| (6) | t: | (von 2) | |||
| (7) | t: | (von 2) | |||
| (8) | f: | (von 6) | (9) | t: | (von 6) |
| X wid. 7, 8 | |||||
| (10) | t: | (von 9) | |||
| (11) | t: | (von 9) | |||
| X wid. 4, 11 | |||||
Beispiel A/5[Bearbeiten | Quelltext bearbeiten]
Beweisen Sie die prädikatenlogische Formel
mittels Resolution.
Lösung[Bearbeiten | Quelltext bearbeiten]
TODO
Beispiel A/6[Bearbeiten | Quelltext bearbeiten]
Geben Sie an, ob die folgenden Aussagen richtig oder falsch sind, und begründen Sie Ihre Antworten. (Zwei Punkte für richtige Antworten mit richtiger Begründung, einen Punkt für richtige Antworten mit leicht mangelhafter Begründung, keinen Punkt für falsche Antworten oder fehlerhafte Begründungen.) (10 Punkte)
| a) | Eine erfüllbare aussagenlogische Formel kann durch Instanziierung (d.h. Anwendung einer Substitution) unerfüllbar werden. | ☒ richtig ☐ falsch |
| b) | Die Menge der unerfüllbaren prädikatenlogischen Formeln ist rekursiv aufzählbar. | ☐ richtig ☐ falsch |
| c) | Wenn bzgl. einer gegebenen prädikatenlogischen Formel F (ohne frei vorkommende Variablen) ein geschlossenes Tableau für f: F existiert, so ist F widerlegbar. | ☐ richtig ☒ falsch |
| d) | Die prädikatenlogischen Formeln und sind logisch äquivalent. | ☐ richtig ☒ falsch |
| e) | Jede aussagenlogische Formel, die nur Variablensymbole und als logische Operatoren höchstens und enthält sowie eine gerade Anzahl von hat, ist erfüllbar. | ☐ richtig ☒ falsch |
Begründung für Punkt a)
TODO
Begründung für Punkt b)
TODO
Begründung für Punkt c)
TODO
Begründung für Punkt d)
Gegenbeispiel - P(x) x ist eine gerade Zahl ; Q(x) x ist eine ungerade Zahl
Begründung für Punkt e)
Gegenbeispiel - unerfüllbar: (A AND NOT(A) AND NOT(A))