Zeigen Sie, dass die Funktion  gemäß
gemäß
 mit
mit 
als Parametrisierung der Oberfläche eines Torus angesehen werden kann. Erklären Sie diese Darstellung anhand einer geeigneten Skizze. Wie lautet die Jakobi-Matrix dieser Funktion?
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier:
Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
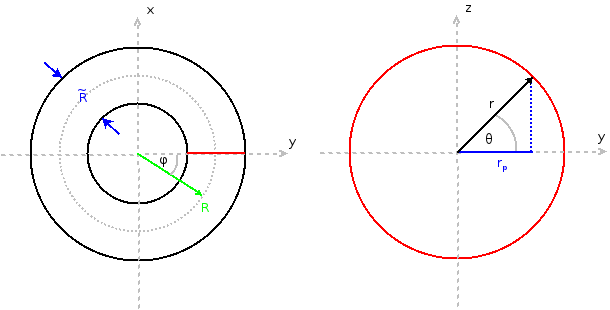
Die Oberfläche eines Torus kann man mit Hilfe von zwei Kreisen konstruieren. Einen Basiskreis mit dem Radius  (linkes Bild) und einen kleineren Kreis mit Radius
(linkes Bild) und einen kleineren Kreis mit Radius  den man um den Basiskreis rotieren lässt (rechtes Bild, Querschnitt der links als rote Linie dargestellt ist).
den man um den Basiskreis rotieren lässt (rechtes Bild, Querschnitt der links als rote Linie dargestellt ist).
Zuerst erfasst man alle Punkte der xy-Ebene: Dies ist eine 2-Dimensionelle Ring-Fläche mit dem variablen Radius  . Parametrisiert erfasst man also alle Koordinaten der x- und y-Achse durch:
. Parametrisiert erfasst man also alle Koordinaten der x- und y-Achse durch:

Übrig bleibt der Wert an der z-Achse. Er ergibt sich aus  und dem Winkel
und dem Winkel  :
:

Zusammengefasst:

 ist abhängig von der Projektion
ist abhängig von der Projektion  des Radius
des Radius  auf die y-Achse , der wiederum ist abhängig vom Winkel
auf die y-Achse , der wiederum ist abhängig vom Winkel  :
:

Eingesetzt ergibt das:


