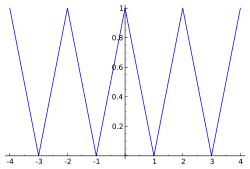
Die Funktion f ( t ) = 1 − t {\displaystyle f(t)=1-t} 0 < t < 1 {\displaystyle 0<t<1} ( − 1 , + 1 ) {\displaystyle (-1,+1)} 2 {\displaystyle 2}
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier:
Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Plot der geraden Funktion
c
0
=
1
T
∫
0
T
f
(
t
)
e
−
i
0
ω
t
d
t
=
1
T
∫
0
T
f
(
t
)
d
t
=
1
T
∫
−
T
2
T
2
f
(
t
)
d
t
=
1
2
∫
−
1
1
f
(
t
)
d
t
=
1
2
(
∫
−
1
0
f
(
t
)
d
t
+
∫
0
1
f
(
t
)
d
t
)
=
1
2
(
∫
−
1
0
(
1
+
t
)
d
t
+
∫
0
1
(
1
−
t
)
d
t
)
=
1
2
(
∫
−
1
0
(
1
+
t
)
d
t
+
∫
0
1
(
1
−
t
)
d
t
)
=
1
2
(
(
t
+
t
2
2
)
|
−
1
0
+
(
t
−
t
2
2
)
|
0
1
)
=
1
2
(
0
+
0
−
(
−
1
)
−
(
−
1
)
2
2
+
1
−
1
2
2
−
0
−
0
)
=
1
2
(
1
−
1
2
+
1
−
1
2
)
=
1
2
{\displaystyle {\begin{aligned}c_{0}&={\frac {1}{T}}\int _{0}^{T}f(t)e^{-i0\omega t}\,\mathrm {d} t\\&={\frac {1}{T}}\int _{0}^{T}f(t)\,\mathrm {d} t\\&={\frac {1}{T}}\int _{-{\frac {T}{2}}}^{\frac {T}{2}}f(t)\,\mathrm {d} t\\&={\frac {1}{2}}\int _{-1}^{1}f(t)\,\mathrm {d} t\\&={\frac {1}{2}}\left(\int _{-1}^{0}f(t)\,\mathrm {d} t+\int _{0}^{1}f(t)\,\mathrm {d} t\right)\\&={\frac {1}{2}}\left(\int _{-1}^{0}(1+t)\,\mathrm {d} t+\int _{0}^{1}(1-t)\,\mathrm {d} t\right)\\&={\frac {1}{2}}\left(\int _{-1}^{0}(1+t)\,\mathrm {d} t+\int _{0}^{1}(1-t)\,\mathrm {d} t\right)\\&={\frac {1}{2}}\left(\left.\left(t+{\frac {t^{2}}{2}}\right)\right|_{-1}^{0}+\left.\left(t-{\frac {t^{2}}{2}}\right)\right|_{0}^{1}\right)\\&={\frac {1}{2}}\left(0+0-(-1)-{\frac {(-1)^{2}}{2}}+1-{\frac {1^{2}}{2}}-0-0\right)\\&={\frac {1}{2}}\left(1-{\frac {1}{2}}+1-{\frac {1}{2}}\right)\\&={\frac {1}{2}}\end{aligned}}}
c
k
=
1
T
∫
0
T
f
(
t
)
e
−
i
k
ω
t
d
t
=
1
T
∫
−
T
2
T
2
f
(
t
)
e
−
i
k
ω
t
d
t
=
1
2
∫
−
1
1
f
(
t
)
e
−
i
k
ω
t
d
t
=
1
2
(
∫
−
1
0
f
(
t
)
e
−
i
k
ω
t
d
t
+
∫
0
1
f
(
t
)
e
−
i
k
ω
t
d
t
)
=
1
2
(
∫
−
1
0
(
1
+
t
)
e
−
i
k
ω
t
d
t
+
∫
0
1
(
1
−
t
)
e
−
i
k
ω
t
d
t
)
=
1
2
(
∫
−
1
0
e
−
i
k
ω
t
+
t
e
−
i
k
ω
t
d
t
+
∫
0
1
e
−
i
k
ω
t
−
t
e
−
i
k
ω
t
d
t
)
=
1
2
(
(
i
e
−
i
k
π
t
k
π
+
(
1
+
i
k
π
t
)
e
−
i
k
π
t
k
2
π
2
)
|
−
1
0
+
(
i
e
−
i
k
π
t
k
π
−
(
1
+
i
k
π
t
)
e
−
i
k
π
t
k
2
π
2
)
|
0
1
)
=
1
2
k
2
π
2
(
(
i
k
π
+
1
+
i
k
π
t
)
e
−
i
k
π
t
|
−
1
0
+
(
i
k
π
−
1
−
i
k
π
t
)
e
−
i
k
π
t
|
0
1
)
=
1
2
k
2
π
2
(
i
k
π
e
−
i
k
π
0
+
e
−
i
k
π
0
+
i
k
π
0
e
−
i
k
π
0
−
i
k
π
e
i
k
π
−
e
i
k
π
+
i
k
π
e
i
k
π
+
i
k
π
e
−
i
k
π
−
e
−
i
k
π
−
i
k
π
e
−
i
k
π
−
i
k
π
e
−
i
k
π
0
+
e
−
i
k
π
0
+
i
k
π
0
e
−
i
k
π
0
)
=
1
2
k
2
π
2
(
i
k
π
+
1
+
0
−
i
k
π
e
i
k
π
−
e
i
k
π
+
i
k
π
e
i
k
π
+
i
k
π
e
−
i
k
π
−
e
−
i
k
π
−
i
k
π
e
−
i
k
π
−
i
k
π
+
1
+
0
)
=
1
2
k
2
π
2
(
2
−
e
i
k
π
⏟
=
(
−
1
)
k
−
e
−
i
k
π
⏟
=
(
−
1
)
k
)
=
2
−
2
(
−
1
)
k
2
k
2
π
2
=
1
−
(
−
1
)
k
k
2
π
2
{\displaystyle {\begin{aligned}c_{k}&={\frac {1}{T}}\int _{0}^{T}f(t)e^{-ik\omega t}\,\mathrm {d} t\\&={\frac {1}{T}}\int _{-{\frac {T}{2}}}^{\frac {T}{2}}f(t)e^{-ik\omega t}\,\mathrm {d} t\\&={\frac {1}{2}}\int _{-1}^{1}f(t)e^{-ik\omega t}\,\mathrm {d} t\\&={\frac {1}{2}}\left(\int _{-1}^{0}f(t)e^{-ik\omega t}\,\mathrm {d} t+\int _{0}^{1}f(t)e^{-ik\omega t}\,\mathrm {d} t\right)\\&={\frac {1}{2}}\left(\int _{-1}^{0}(1+t)e^{-ik\omega t}\,\mathrm {d} t+\int _{0}^{1}(1-t)e^{-ik\omega t}\,\mathrm {d} t\right)\\&={\frac {1}{2}}\left(\int _{-1}^{0}e^{-ik\omega t}+te^{-ik\omega t}\,\mathrm {d} t+\int _{0}^{1}e^{-ik\omega t}-te^{-ik\omega t}\,\mathrm {d} t\right)\\&={\frac {1}{2}}\left(\left.\left({\frac {ie^{-ik\pi t}}{k\pi }}+{\frac {(1+ik\pi t)e^{-ik\pi t}}{k^{2}\pi ^{2}}}\right)\right|_{-1}^{0}+\left.\left({\frac {ie^{-ik\pi t}}{k\pi }}-{\frac {(1+ik\pi t)e^{-ik\pi t}}{k^{2}\pi ^{2}}}\right)\right|_{0}^{1}\right)\\&={\frac {1}{2k^{2}\pi ^{2}}}\left(\left.\left(ik\pi +1+ik\pi t\right)e^{-ik\pi t}\right|_{-1}^{0}+\left.\left(ik\pi -1-ik\pi t\right)e^{-ik\pi t}\right|_{0}^{1}\right)\\&={\frac {1}{2k^{2}\pi ^{2}}}\left(ik\pi e^{-ik\pi 0}+e^{-ik\pi 0}+ik\pi 0e^{-ik\pi 0}-ik\pi e^{ik\pi }-e^{ik\pi }+ik\pi e^{ik\pi }+ik\pi e^{-ik\pi }-e^{-ik\pi }-ik\pi e^{-ik\pi }-ik\pi e^{-ik\pi 0}+e^{-ik\pi 0}+ik\pi 0e^{-ik\pi 0}\right)\\&={\frac {1}{2k^{2}\pi ^{2}}}\left(ik\pi +1+0-ik\pi e^{ik\pi }-e^{ik\pi }+ik\pi e^{ik\pi }+ik\pi e^{-ik\pi }-e^{-ik\pi }-ik\pi e^{-ik\pi }-ik\pi +1+0\right)\\&={\frac {1}{2k^{2}\pi ^{2}}}\left(2-\underbrace {e^{ik\pi }} _{=(-1)^{k}}-\underbrace {e^{-ik\pi }} _{=(-1)^{k}}\right)\\&={\frac {2-2(-1)^{k}}{2k^{2}\pi ^{2}}}\\&={\frac {1-(-1)^{k}}{k^{2}\pi ^{2}}}\end{aligned}}}
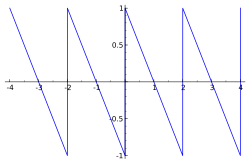
Plot der ungeraden Funktion c 0 = 1 T ∫ 0 T f ( t ) e − i 0 ω t d t = 1 2 ∫ 0 2 f ( t ) d t = 1 2 ∫ 0 2 ( 1 − t ) d t = 1 2 ( t − t 2 2 ) | 0 2 = 1 2 ( 2 − 2 2 2 − 0 + 0 ) | 0 2 = 0 {\displaystyle {\begin{aligned}c_{0}&={\frac {1}{T}}\int _{0}^{T}f(t)e^{-i0\omega t}\,\mathrm {d} t\\&={\frac {1}{2}}\int _{0}^{2}f(t)\,\mathrm {d} t\\&={\frac {1}{2}}\int _{0}^{2}(1-t)\,\mathrm {d} t\\&={\frac {1}{2}}\left.\left(t-{\frac {t^{2}}{2}}\right)\right|_{0}^{2}\\&={\frac {1}{2}}\left.\left(2-{\frac {2^{2}}{2}}-0+0\right)\right|_{0}^{2}\\&=0\end{aligned}}}
c
k
=
1
T
∫
0
T
f
(
t
)
e
−
i
k
ω
t
d
t
=
1
2
∫
0
2
f
(
t
)
e
−
i
k
π
t
d
t
=
1
2
∫
0
2
(
1
−
t
)
e
−
i
k
π
t
d
t
=
1
2
∫
0
2
e
−
i
k
π
t
−
t
e
−
i
k
π
t
d
t
=
1
2
(
i
e
−
i
k
π
t
k
π
−
(
1
+
i
k
π
t
)
e
−
i
k
π
t
k
2
π
2
)
|
0
2
=
1
2
k
2
π
2
(
i
k
π
−
1
−
i
k
π
t
)
e
−
i
k
π
t
|
0
2
=
1
2
k
2
π
2
(
i
k
π
e
−
i
k
π
2
−
e
−
i
k
π
2
−
i
k
π
2
e
−
i
k
π
2
−
i
k
π
e
−
i
k
π
0
+
e
−
i
k
π
0
+
i
k
π
0
e
−
i
k
π
0
)
=
1
2
k
2
π
2
(
i
k
π
−
1
−
i
k
π
2
−
i
k
π
+
1
+
0
)
=
−
i
k
π
2
2
k
2
π
2
=
−
i
k
π
{\displaystyle {\begin{aligned}c_{k}&={\frac {1}{T}}\int _{0}^{T}f(t)e^{-ik\omega t}\,\mathrm {d} t\\&={\frac {1}{2}}\int _{0}^{2}f(t)e^{-ik\pi t}\,\mathrm {d} t\\&={\frac {1}{2}}\int _{0}^{2}(1-t)e^{-ik\pi t}\,\mathrm {d} t\\&={\frac {1}{2}}\int _{0}^{2}e^{-ik\pi t}-te^{-ik\pi t}\,\mathrm {d} t\\&={\frac {1}{2}}\left.\left({\frac {ie^{-ik\pi t}}{k\pi }}-{\frac {(1+ik\pi t)e^{-ik\pi t}}{k^{2}\pi ^{2}}}\right)\right|_{0}^{2}\\&={\frac {1}{2k^{2}\pi ^{2}}}\left.(ik\pi -1-ik\pi t)e^{-ik\pi t}\right|_{0}^{2}\\&={\frac {1}{2k^{2}\pi ^{2}}}\left(ik\pi e^{-ik\pi 2}-e^{-ik\pi 2}-ik\pi 2e^{-ik\pi 2}-ik\pi e^{-ik\pi 0}+e^{-ik\pi 0}+ik\pi 0e^{-ik\pi 0}\right)\\&={\frac {1}{2k^{2}\pi ^{2}}}\left(ik\pi -1-ik\pi 2-ik\pi +1+0\right)\\&={\frac {-ik\pi 2}{2k^{2}\pi ^{2}}}\\&={\frac {-i}{k\pi }}\end{aligned}}}