TU Wien:Analysis 2 UE (diverse)/Übungen SS23/Beispiel 107
Zur Navigation springen
Zur Suche springen
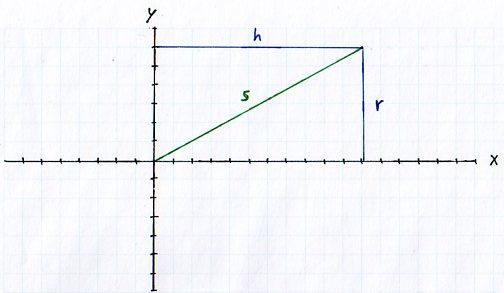
Gegeben ist ein Kegel mit Höhe h und Basiskreisradius r. Berechnen Sie die Mantelfläche, indem Sie den Kegel als Rotationskörper interpretieren.
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
Eine Gerade die durch den Koordinatenursprung verläuft und sich um die x-Achse dreht, bildet einen Kegel.
Die Gerade können wir mittels ihren Anstieg beschreiben, also: , mit
Es gilt außerdem (Wird für die Herleitung von benötigt.)
Nun setzen wir diese Funktion in der Formel zur Berechnung von Mantelflächen von Rotationskörpern (siehe Mathematik für Informatik S.258)