TU Wien:Einführung in wissensbasierte Systeme VU (Egly)/Prüfung 2012-11-12

Angabe

Beispiel 1 : Logikbasierte Wissensrepräsentation

a

Sei $\phi$ eine geschlossene prädikatenlogische Formel, die eine Wissesnbasis darstellt, und sei $\psi$ eine geschlossene prädikatenlogische Formel, die eine Anfrage repräsentiert. Ihr Chef kaufte einen Theorembeweiser für Prädikatenlogik, der auf dem Tableaukalkül in Negationsnormalform basiert. Sie sollen nun eine Übersetzung angeben, die Entailment-Probleme der Form $\phi \models \psi$ in einen Input verwandelt, der von dem Solver akzeptiert wird.

Geben Sie Ihre Übersetzung an und beschreiben Sie die Übersetzungsschritte möglichst detailliert. Erklären Sie auch die logische Beziehung zwischen den Inputs und den Outputs der einzelnen Schritte.

(5 Punkte)

b

Kreuzen Sie zutreffendes [richtig oder falsch] an ($\phi$ und $\psi$ sind Formeln)

1. Wenn die Formel $\psi$ erfüllbar, aber nicht gültig ist, so ist $\psi \rightarrow \neg \psi$ ebenfalls erfüllbar.
2. Wenn $\phi \models \psi$ gilt, so sind alle Modelle von $\psi$ auch Modelle von $\phi$.
3. Wenn die Formel $\phi \rightarrow \neg \psi$ gültig ist, dann ist auch $\phi \lor \psi$ erfüllbar.
4. Wenn die Formel $\phi \rightarrow \psi$ gültig und $\neg \psi$ erfüllbar, aber nicht gültig ist, so muß $\phi$ unerfüllbar sein.

(8 Punkte)

c

Zeigen sie die folgenden Aussagen mittels Semantik:

1. $\phi \models \psi$ gdw $\models \phi \rightarrow \psi$
2. $\models \phi \rightarrow \psi$ gdw $\phi \land \neg \psi$ unerfüllbar ist.

(10 und 7 Punkte)

Beispiel 2 : Nichtmonotones Schließen

a

Was versteht man unter der Nichtmonotonie einer Inferenzrelation?

(5 Punkte)

b

Geben Sie eine aussagenlogische Theorie $T$ an, sodass folgende zwei Bedingungen gleichzeitig erfüllt sind:

1. die CWA von $T$ ist inkonsistent.
2. die CWA von $T$ relativ zu $p$ ist konsistent (wobei $p$ ein Atom ist).

(5 Punkte)

c

Gegeben ist folgende Wissensbasis $T$ über einer Sprache mit den einzigen Konstantensymbolen $a,b,c$, dem Variablensymbol $x$ und den einzigen Prädikatensymbolen $P$ und $Q$:

$T=\left\lbrace \exists xQ(x),P(a),\neg Q(b),\forall x(P(x)\rightarrow Q(x))\right\rbrace$

Geben sie die Elemente der Closed-World Assumption ${\text{CWA}}(T)$ von $T$ an, indem Sie folgende Gleichungen ergänzen:

1. $T_{asm}=\{...\}$
2. ${\text{CWA}}(T)=\{\psi |...\}$

(4 Punkte)

d

Geben Sie die Definition des klassischen Redukts $\Delta _{E}$ einer Menge $\Delta$ von geschlossenen Defaults bezüglich einer Menge $E$ von geschlossenen Formeln an.

(4 Punkte)

e

Gegeben seien folgende Mengen ($p,q,r,s$ sind aussagenlogische Konstanten):

$\Delta =\left\lbrace {\frac {r:\neg s}{\neg p}},{\frac {s,q:\neg r}{r}},{\frac {\neg r:q,s}{s}},{\frac {:\neg s}{p}},\right\rbrace$

${\begin{aligned}W_{1}&=\{r\},&W_{2}&=\{r,\neg p\},&W_{3}&=\{s,q\}\\E_{1}&=Cn(W_{1}\cup \{\neg q,p\}),&E_{2}&=Cn(W_{2}),&E_{3}&=Cn(W_{3}\cup \{\neg r,p\})\end{aligned}}$

• (6 Punkte) Geben Sie die klassischen Redukte $\Delta _{E_{i}}$ von $\Delta$ bezüglich den Mengen $E_{i}$ an, für $i=1,2,3$.
• (6 Punkte) Markieren sie die korrekten Aussagen:
  1. $E_{1}$ ist eine Extension der Default Theorie $T_{1}=(W_{1},\Delta )$
  2. $E_{2}$ ist eine Extension der Default Theorie $T_{2}=(W_{2},\Delta )$
  3. $E_{3}$ ist eine Extension der Default Theorie $T_{3}=(W_{3},\Delta )$

Beispiel 3 : Answer-Set Programmierung

a

Sei $M$ eine Interpretation und $P$ ein grundiertes Programm.

1. Definieren Sie den Begriff des Reduktes $P^{M}$.
2. Wann ist $M$ ein Answer Set von $P$?

(8 Punkte)

b

Betrachten Sie folgendes Programm ($a,b,c,d$ sind Grundatome)

${\begin{aligned}P=\{&a\lor \neg c:-\,\,,\\&c\lor \neg d:-\,\,,\\&c\lor a:-\,b,\\&a\lor b:-\,\,\}\end{aligned}}$

Geben Sie eine Menge $Q$ von Constraints an sodass $P\cup Q$ nur $\{a,c\}$ als Answer Set besitzt.

(6 Punkte)

c

Was versteht man unter einer abduktiven Diagnose eines abduktiven Diagnose Problems $\langle H,T,O\rangle$?

(5 Punkte)

d

In welcher Weise kann ein grundiertes, normales Program P als Default Theorie T übersetzt werden, sodass die Answer Sets von P zu den Extensionen von T korresponideren?

(5 Punkte)

e

Welche der folgenden Eigenschaften treffen zu [richtig, falsch]?

1. In ASP entsprechen Beweise, und nicht Modelle, der Lösung eines Suchproblems.
2. Jedes Answer Set eines Programms P ist ein klassisches Modell von P.
3. Das Programm $P=\{a\lor b:-\,\,,a\lor c:-\,\,\}$ hat zwei Answer Sets.

(6 Punkte)

Beispiel 4 : Probabilistisches Schließen

a

Was versteht man unter dem Begriff Marginalisation im probabilistischen Schließen? Geben Sie ein kurzes Beispiel.

(6 Punkte)

b

Leiten Sie das Bayes'sche Gesetz aus der Produktregel her.

(6 Punkte)

c

Was ist ein Bayes'sches Netz (Grundidee, Komponenten)? Welche Unabhängigkeitsannahmen gelten in einem Bayes'schen Netz?

(8 Punkte)

d

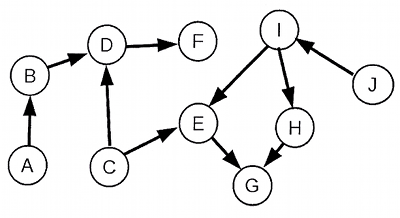
Gegeben ist folgender Graph eines Bayes'schen Netzes:

Welche der folgenden Eigenschaften treffen zu [richtig, falsch]:

1. E ist nicht bedingt unabhängig von H bei Evidenz B.
2. F ist bedingt unabhängig von A bei Evidenz B.
3. D ist bedingt unabhängig von A bei Evidenz J.
4. C ist bedingt unabhängig von H bei Evidenz D.

(10 Punkte)

Ausarbeitung

Beispiel 1 : Logikbasierte Wissensrepräsentation

a

Allgemein: Die NNF ist eine Umformung, sodass gilt: nnf($\phi$) = $\phi$ (in semantischer Hinsicht)

Eine Formel in NNF hat folgende Eigenschaften:

1. Negationen stehen nur direkt vor Atomen
2. Es gibt nur die Operatoren $\land$ und $\lor$

Umwandlungsschritte:

1. Umwandlung von Implikationen: Input = $\phi \rightarrow \psi$ Output = $\neg \phi \lor \psi$

Kann jemand, die/der sich mit tex auskennt, weiterhelfen? Ich komme mit den Tex-Ausdrücken nicht weiter, verstehe nicht, warum das nicht geht!

--GeorgScholz (Diskussion) 09:35, 16. Jan. 2013 (CET)

b

Allgemein gilt:

• gültig: die Formel ergibt unter allen Intepretationen true
• erfüllbar: Es gibt mindestens eine Interpretation, unter die Formel true ergibt
• erfüllbar, aber nicht gültig: Es gibt mindestens eine Interpretation, unter die Formel true ergibt UND es gibt mindestens eine Interpretation, unter die Formel false ergibt

Lösungen:

1. richtig
2. falsch (alle Modelle von $\phi$ sind Modelle von $\psi$)
3. FALSCH! In der Angabe steht ja nur, dass die Implikation valid ist. Das sagt somit aus, dass jede Interpretation von I(a->b) TRUE ergibt, es sagt aber nichts daraus aus, wie die Interpretation der Einzelformeln evaluieren. Es könnte also sein, das jede Interpretation I(a) und I(b) FALSE ergibt. Die Implikation wäre dann nach wie gültig, jedoch wäre die Oder-Verknüpfung dann false.
   
   [vik_xxxl Vorschlag:] ich bin nicht sicher dass es FALSCH ist. Es ist eher WAHR.
   F1= a=>-b evaluiert zu 0 nur wenn a=1,b=1 und nachdem es gegeben ist dass F1= a=>-b gültig ist, darf F1 nicht 0 sein und somit bleiben nur 3 mögliche interpretation für F1= a V b zu beachten und zwar (a,b) € {(1,0),(0,1),(0,0)}. Also diese drei interpretationen sind ALLE mögliche interpretationen für F2= a V b. Nun ist F2= a V b erfülbar, weil es gibt zwei interpretationen die zu 1 evaluieren. Ausserdem ist F2 auch falsifiable weil es eine interpretation gibt die zu 0 evaluiert, aber F2 ist weder unerfülbar noch gültig.
4. falsch

c

1. siehe TU_Wien:Einführung in wissensbasierte Systeme VU (Egly)/Beweissammlung#Deduction theorem
2. siehe TU_Wien:Einführung in wissensbasierte Systeme VU (Egly)/Beweissammlung#Prüfung 2012-11-12 Beispiel 1. c) 2.

Beispiel 2 : Nichtmonotones Schließen

a

Was versteht man unter der Nichtmonotonie einer Inferenzrelation?

Eine Inferenczrelation $\vdash$ erfüllt Nichtmonotonie wenn es eine Theroie $\Gamma$ und Formeln $\varphi$,$\psi$ gibt für die gilt $\Gamma \vdash \varphi$ nicht aber $\Gamma$,$\psi \vdash \varphi$.

(5 Punkte)

b

$T=\{p\lor q\}$

c

1. $T_{asm}=\{\neg P(b),\neg P(c),\neg Q(c)\}$
2. ${\text{CWA}}(T)=\{\psi \mid T\cup T_{asm}\models \psi ,\psi {\text{ closed }}\}$

d

$\Delta _{E}=\{\varphi /\gamma \mid \varphi :\neg \psi _{1},...,\neg \psi _{n}/\gamma \in \Delta ,\{\psi _{1},...,\psi _{n}\}\cap E=\emptyset \}$

e

• $\Delta _{E_{i}}$
  1. $\{r/\neg p,\top /p\}$
  2. $\{r/\neg p,\neg r/s,\top /p\}$
  3. $\{(s,q)/r,\neg r/s\}$

• Ist $E_{i}$ eine Extension der Default Theorie $T_{i}=(W_{i},\Delta )$:
  1. falsch
  2. falsch
  3. falsch

Beispiel 3 : Answer-Set Programmierung

a

1. $P^{M}=\{a_{1}\lor ...\lor a_{m}:-\,\,b_{1},...,b_{k}\mid a_{1}\lor ...\lor a_{m}:-\,\,b_{1},...,b_{k},not\,b_{k+1},...,not\,b_{n}\in P,\{b_{k+1},...,b_{n}\}\cap M=\emptyset \}$
2. Wenn $M$ ein minimales Modell von $P^{M}$ ist.

b

$P$ hat die Answer sets $\{a,c\},\{a,\neg d\}$

$\{a,\neg d\}$ wollen wir eliminieren also:

$Q=\{:-\neg d\}$ oder $Q=\{:-not\,c\}$

c

Eine Menge $S\subseteq H$ so dass $T\cup S\models O$ gilt. ($\models$ "brave consequence relation")

d

Ist $r\in P$ eine Regel der Form

$a:-\,b_{1},...,b_{n},not\,c_{1},...,not\,c_{m}$

dann ist $\delta (r)$ die korrespondierende Default-Regel ${\frac {b_{1}\lor ...\lor b_{n}:\neg c_{1},...,\neg c_{m}}{a}}$

Sei $\delta (P)=\{\delta (r)\mid r\in P\}$ dann kann das Programm $P$ als Default-Theorie $T=(\emptyset ,\delta (P))$ dargestellt werden, womit die Answer Sets von P zu den Extensionen von T korresponideren.

e

1. falsch
2. richtig
3. richtig: $\{a\},\{b,c\}$

Beispiel 4 : Probabilistisches Schließen

a

Was versteht man unter dem Begriff Marginalisation im probabilistischen Schließen? Geben Sie ein kurzes Beispiel.

(6 Punkte)

Theorie:

Extracting the distribution over some subset of a given set of variables is called marginalisation.

$P(V_{i_{1}}=v_{i_{1}},...,V_{i_{k}}=v_{i_{k}})=\sum _{V_{i_{1}}=v_{i_{1}},...,V_{i_{k}}=v_{i_{k}}}P(V_{1},...,V_{n})$

Beispiel:

2 Boolean-Variablen: r ... rich, f ... famous

$P(R=r)=P(r,f)+P(r,\neg f)$

b

Produktregel:

$P(V_{1},..,V_{n}\mid {\boldsymbol {V}})=\prod _{i=1}^{n}P(V_{i}\mid V_{i+1},...,V_{n},{\boldsymbol {V}})$

Herleitung:

$P(A,B)=P(A\mid B)P(B)$

$P(B,A)=P(B\mid A)P(A)$

$P(A,B)=P(B,A)$

$P(A\mid B)P(B)=P(B\mid A)P(A)$

$P(A\mid B)={\frac {P(B\mid A)P(A)}{P(B)}}$

c

Was ist ein Bayes'sches Netz (Grundidee, Komponenten)? Welche Unabhängigkeitsannahmen gelten in einem Bayes'schen Netz?

(8 Punkte)

d

1. richtig
2. richtig
3. falsch
4. richtig // Lösungsvorschlag2[vik_xxxl]: es kann nicht richtig sein. C-E-I-H ist nicht blockiert => NICHT bedingt unabhängig.

// [adotw] Lösung für d #4: doch, ist richtig da E nicht in der Evidenzmenge ist und zwei eingehende Pfade hat und somit blockiert

Materialien

Neues Material hinzufügen

B

• bayes-network.png (details)