TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 211
Zur Navigation springen
Zur Suche springen
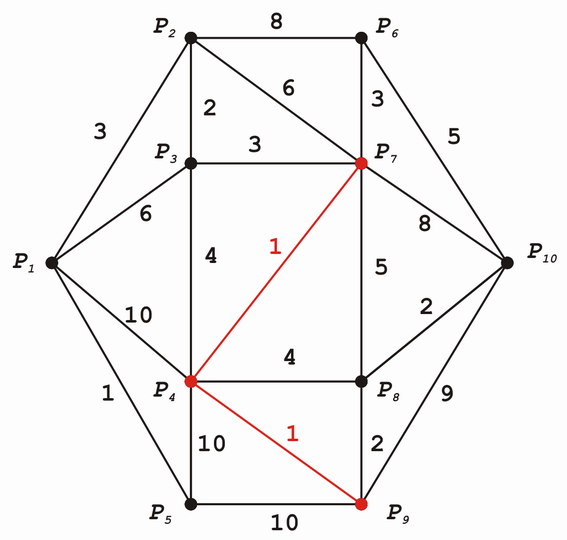
In der folgenden schematisch skizzierten Landkarte sind für eine bestimmte Fracht die Transportkosten zwischen den einzelnen Orten angegeben. Welches ist der billigste Weg vom Ort zum Ort ?
Theorie - Algorithmus von Dijkstra[Bearbeiten | Quelltext bearbeiten]
Siehe TU_Wien:Mathematik_1_UE_(diverse)/Theorie_WS05/06.12.2005_Graphentheorie!
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Basierend auf f.thread:37700
Tabellarische Lösung[Bearbeiten | Quelltext bearbeiten]
| Iteration | Auswahl | Vorgänger | ||||||||||
| 0 | 0 | |||||||||||
| 1 | 3 | 6 | 10 | 1 | ||||||||
| 2 | 3 | 6 | 10 | 11 | ||||||||
| 3 | 5 | 11 | 9 | 11 | ||||||||
| 4 | 9 | 8 | ||||||||||
| 5 | 9 | 11 | 13 | 16 | ||||||||
| 6 | 13 | 10 | ||||||||||
| 7 | 12 | 16 | ||||||||||
| 8 | 14 |
Kürzester Weg somit:
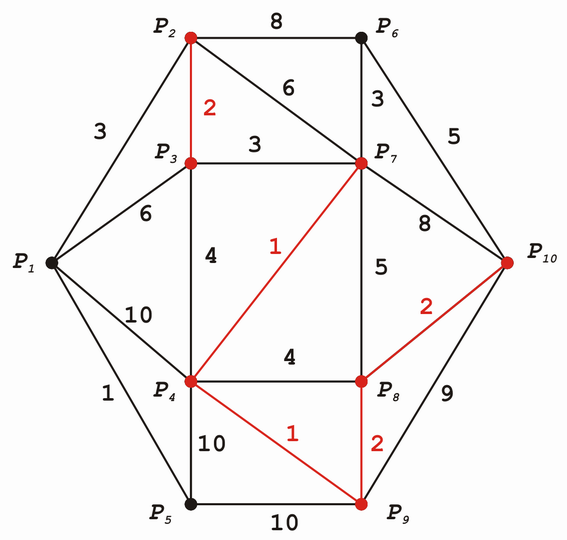
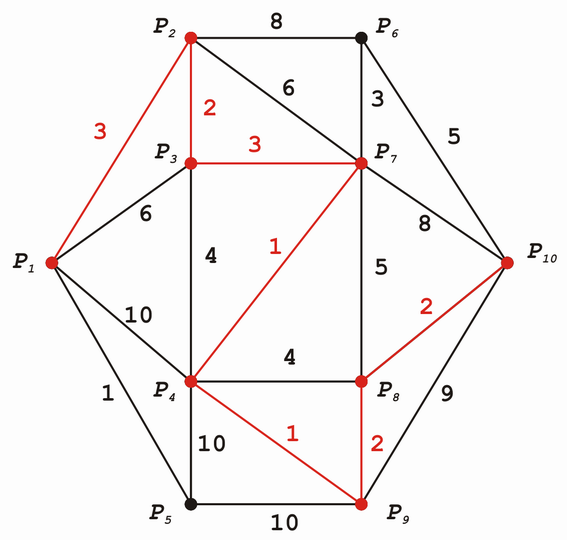
Edit: es gibt noch einen zweiten möglichen kürzesten Weg: