TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 121

Sei $T_{70}$ die Menge alle natürlichen Zahlen, die 70 teilen. Man vergleiche die Hassediagramme der beiden Halbordnungen $\langle {\mathcal {P}}(\{a,b,c\}),\subseteq \rangle$ und $\langle T_{70},|\rangle$.

Dieses Beispiel ist als solved markiert. Ist dies falsch oder ungenau? Aktualisiere den Lösungsstatus (Details: Vorlage:Beispiel)

Lösung für $\langle {\mathcal {P}}(\{a,b,c\}),\subseteq \rangle$:

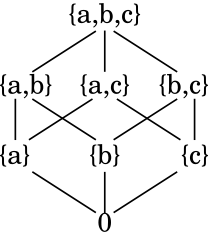
Die Potenzmenge der Menge {a,b,c}, also ${\mathcal {P}}(\{a,b,c\})=\{\emptyset ,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\}$.

Das Hasse-Diagramm sieht daher wie folgt aus:

Das bedeutet: $\emptyset \subseteq \{a\}$, $\emptyset \subseteq \{b\}$, $\emptyset \subseteq \{c\}$, $\{a\}\subseteq \{a,b\}$ etc.

Lösung für $\langle T_{70},|\rangle$:

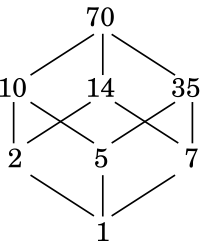
Die Menge $T_{70}$ bezeichnet die Menge aller Teiler von 70. Alle Zahlen sind durch 1 und durch sich selbst teilbar. Nicht-Primzahlen wie 70 sind zusätzlich noch durch ihre Primfaktoren (in diesem Fall 2, 5 und 7) und durch die Kombinationen dieser Primfaktoren ($2\cdot 5=10$, $2\cdot 7=14$, $5\cdot 7=35$) teilbar. Daher ist

$T_{70}=\{1,2,5,7,10,14,35,70\}$

Das Hasse-Diagramm dazu:

(Von Deez):

Das bedeutet: $1|2$, $1|5$, $1|7$, $2|10$, $2|14$ etc.

Die Ähnlichkeit sehe ich wie folgt: Setzt man die Mengen wie folgt {1,2,5,7} {0,a,b,c} und sieht das als 1 = 0 (leere menge) 2 = a 5 = b 7 = c

und damit löst sich das gesamten Hasse Diagramme ineinander auf: 70 = {a,b,c} = 2 * 5 * 7 14 = 2*7 = {a,c}

Das heißt < P(2,5,7), *> (ich hoff ich hab das formal richtig definiert) deckt sich mit der Definition von < P(a,b,c), <= ) und 2,5,7 entspricht genau den Primfaktoren von 70!

Nachsatz von Mnemetz : Es handelt sich um einen Isomorphismus!