TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 118

Untersuchen Sie, ob die Relation $ARB\Leftrightarrow A\bigtriangleup B=A$ ($\bigtriangleup$ die symmetrische Differenz) auf der Potenzmenge einer Menge M eine Äquivalenzrelation bildet.

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Hilfreiches

Äquivalenzrelation

Äquivalenzrelation

Eine binäre Relation R auf einer Menge A heißt Äquivalenzrelation, wenn folgende drei Eigenschaften erfüllt sind:

Reflexivität: $\forall a\,\in A:aRa$,

Symmetrie: $\forall a,b\,\in A:aRb\Rightarrow bRa$,

Transitivität: $\forall a,b,c\,\in A:(aRb\wedge bRc)\Rightarrow aRc$.

Mengen-Differenz

Mengen-Differenz

A - B - A\B
e - e - ne
e - ne - e
ne - e - ne
ne - ne - ne


e .... ist Element
ne .... ist kein Element

=)

Reflexivität

Reflexivität

$\forall a\in M:\quad aRa$

Symmetrie

Symmetrie

$\forall a,b\in M:aRb\Rightarrow bRa$

Transitivität

Transitivität

$\forall a,b,c\in M:\quad a\circ b\wedge b\circ c\Rightarrow a\circ c$

Disjunkt

Disjunkte Mengen

Zwei Mengen $A$ und $B$ heißen disjunkt (oder elementfremd), wenn sie keine gemeinsamen Elemente besitzen.

$A,B\;{\text{disjunkt}}\Longleftrightarrow A\cap B=\emptyset$

Mehrere Mengen $M_{i}$ heißen paarweise disjunkt, wenn je zwei Mengen keine gemeinsamen Elemente besitzen.

$\forall i:\forall j\neq i:M_{i}\cap M_{j}=\emptyset$

Definition der symmetrischen Differenz

$A\bigtriangleup B=(A\setminus B)\cup (B\setminus A)$

C heißt symmetrische Differenz der Mengen A und B,

$C=A\triangle B$,

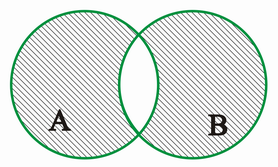
wenn C alle Elemente aus A enthält, die nicht zu B gehören und alle Elemente aus B, die nicht zu A gehören, d.h.:

$A\triangle B=(A-B)\cup (B-A)$

VENN-Diagramm:

Reflexivität

Reflexivität heißt, dass jedes Element in Relation zu sich selbst steht:

die Relation ist definiert : A $\bigtriangleup$ B = A

dh: wenn A in relation mit A steht => A $\bigtriangleup$ A = A

Aber das ergibt nicht A, sondern eine leere Menge => nicht reflexiv

Symmetrie

$ARB\Rightarrow BRA$?

Symmetrie heißt, wenn für alle a,b mit aRb auch bRa folgt.

$\forall {\text{ a,b }}\in {\text{ }}A^{2}:{\text{ (a,b) }}\in {\text{ R }}\qquad \Rightarrow \qquad {\text{ (b,a) }}\in {\text{ R }}$

Aus der Definition der symmetrischen Differenz folgt:

${\begin{array}{rcl}A\bigtriangleup B=A&\Leftrightarrow &B=\emptyset \\B\bigtriangleup A=B&\Leftrightarrow &A=\emptyset \end{array}}$

Daher ist die Relation R nur dann symmetrisch, wenn A = B. D. h. sie ist im allgemeinen nicht symmetrisch.

Transitivität

$ARB\land BRC\Rightarrow ARC$?

Eine Relation R transitiv, wenn stets gilt: (a,b) aus R UND (b,c) aus R FOLGT (a,c) aus R

$\forall {\text{ a,b }}\in {\text{ R }}:{\text{ (a,b) }}\in {\text{ R }}\wedge {\text{ (b,c) }}\in {\text{ R }}\qquad \Rightarrow \qquad {\text{ (a,c) }}\in {\text{ R }}$

Zwei Mengen A und B können entweder disjunkt sein ...

---

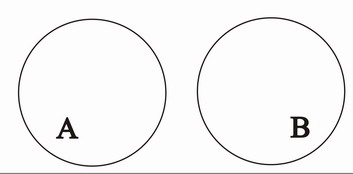
Die Mengen A und B heißen disjunkt, wenn gilt:

$A\cap B=\varnothing$

$\varnothing$ symbolisiert eine leere Menge.

Als VENN-Diagramm dargestellt:

---

... oder sich schneiden. Anhand der oben angeführten Definition der symmetrischen Differenz sieht man leicht, daß $A\bigtriangleup B$ die Menge $A\cup B$ ist, wenn die Mengen disjunkt sind, oder aber die Vereinigung zweier echter Teilmengen von jeweils A und B umfaßt, wenn sie nicht disjunkt sind. Daher kann $A\bigtriangleup B=A$ nur gelten, wenn $B=\emptyset$ und damit $A\bigtriangleup B=A\bigtriangleup \emptyset =(A\setminus \emptyset )\cup (\emptyset \setminus A)=A$ gilt.

Daraus kann man folgern:

${\begin{array}{rcl}A\bigtriangleup B=A&\Longleftrightarrow &B=\emptyset \\B\bigtriangleup C=B&\Longleftrightarrow &C=\emptyset \end{array}}$

Und damit gilt:

$A\bigtriangleup C=A\bigtriangleup \emptyset =A$

Daraus folgt, daß die Relation R transitiv ist.

Anmerkung hauns:

stimmt mMn nicht, denn:

${\begin{array}{rcl}A\bigtriangleup B=A&\Longleftrightarrow &B=\emptyset \\B\bigtriangleup C=B&\Longleftrightarrow &C=\emptyset \end{array}}$

B kann nicht bei ARB die leere Menge sein und dann bei BRC plötzlich nicht mehr die leere Menge sein, es ist ja ein und dieselbe Menge

$A\bigtriangleup B=A\bigtriangleup \emptyset =A\Rightarrow B=\emptyset$

Das bedeutet aber, dass egal was du machst, bei BRC bekommt man als Ergebnis nur die leere Menge, oder C:

${\begin{aligned}C&=\emptyset :\\B\bigtriangleup C&=\emptyset \bigtriangleup \emptyset =\emptyset \\C&=C\\B\bigtriangleup C&=\emptyset \bigtriangleup C=C\end{aligned}}$

für ARB & BRC $\Rightarrow$ ARC würde das aber wegen B = $\emptyset$ bei BRC bereits nicht B ergeben, sondern entweder $\emptyset$ oder C ... daher sicher nicht transitiv

Links

Siehe auch f.thread:23103 , f.thread:22874