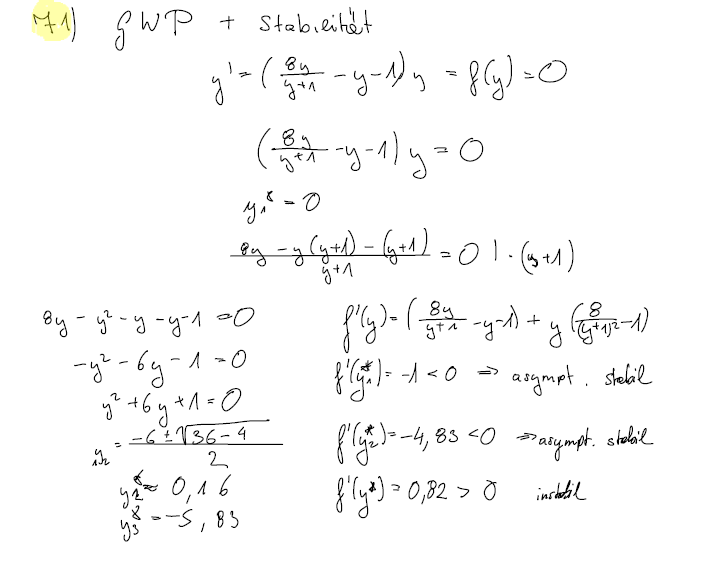TU Wien:Analysis 2 UE (diverse)/Übungen SS23/Beispiel 328
Zur Navigation springen
Zur Suche springen
Man berechne alle möglichen Gleichgewichtslagen der nichtlinearen Differentialgleichung
und überprüfe sie auf Stabilität.
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
Die erste Nullstelle ergibt sich trivial, die anderen beiden sind durch Nullsetzen des Klammerausdrucks erhältlich:
(asymptotisch stabil)
(asymptotisch stabil)
(instabil)
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
Lösungsvorschlag von mnemetz (basierend auf Lösung aus 2004 unten)[Bearbeiten | Quelltext bearbeiten]
Ich habe meinen Lösungsvorschlag (basierend auf Lösung aus 2004 unten) mit LaTex nieder geschrieben und das PDF hier zum Download bereitgestellt. --Markus Nemetz 19:28, 2. Jul 2006 (CEST)
Log der Verbesserungen[Bearbeiten | Quelltext bearbeiten]
- Flüchtigkeitsfehler korr. --Markus Nemetz 12:45, 3. Jul 2006 (CEST)
Lösung aus Karigl 2004[Bearbeiten | Quelltext bearbeiten]
- PDF aus Karigl 2004 --Markus Nemetz 12:05, 19. Jun 2006 (CEST)
Quelle[Bearbeiten | Quelltext bearbeiten]
- Karigl 04 Beispiel 46
- Panholzer Beispielsammlung SS06 Beispiel 164 / SS07 Beispiel 226
- WS 10 Beispiel 56