TU Wien:Analysis VU (diverse)/Übungen 2024S/Beispiel 375
Man bestimme alle relativen Extrema und Sattelpunkte der Funktion im angegebenen Bereich:
für Hinweis: Eine symmetrische 2x2-Matrix ist genau dann indefinit, wenn ihre Determinante negativ ist.
Graph[Bearbeiten | Quelltext bearbeiten]
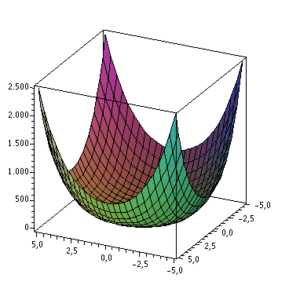
Lösungsvorschlag[Bearbeiten | Quelltext bearbeiten]
Zuerst müssen wir uns die partiellen Ableitungen und ausrechnen.
Dann stellen wir ein Gleichungssystem mit und auf, um alle stationären Punkte zu bestimmen. Dies sind die Punkte, die als Extrema für die Funktion überhaupt infrage kommen würden.
Mir fehlt leider die Zeit, um genauer auszuführen, wie dieses Gleichungssystem gelöst wird. Man verwendet u.a. den Produkt-Null-Satz, welcher bei solchen Beispielen immer äußerst hilfreich ist. Wenn wir es jedenfalls lösen, bekommen wir folgende stationäre Punkte als Lösungen:
Als nächsten Schritt stellen wir die Hesse-Matrix auf. Von dieser Berechnen wir uns dann die Determinante. Wenn die Determinante kleiner als 0 ist, handelt es sich um einen Sattelpunkt. Wenn sie größer als 0 ist, müssen wir uns noch ansehen. Wenn dieses kleiner als 0 ist, handelt es sich um ein relatives Maximum. Wenn es größer als 0 ist, handelt es sich um ein relatives Minimum. Zuerst müssen wir uns jedoch und ausrechnen.
Die Hesse-Matrix sieht also wie folgt aus:
Im folgenden setzen wir jeden Punkt einzeln ein, rechnen die Determinante aus und schauen, was rauskommt.
Für :
Da die Determinante für (0,0) negativ ist, handelt es sich um einen Sattelpunkt.
Für :
Da die Determinante hier größer als 0 ist, müssen wir uns noch ansehen.
Da handelt es sich hier um ein relatives Minimum.
Für :
Da die Determinante hier größer als 0 ist, müssen wir uns noch ansehen.
Da handelt es sich hier um ein relatives Minimum.
Links[Bearbeiten | Quelltext bearbeiten]
- Diskussion im Informatikforum (SS07)
- Diskussion im Informatikforum WS07 Beispiel 123
- Diskussion im Informatikforum (SS08)