TU Wien:Statistik und Wahrscheinlichkeitstheorie VO (Dutter)/Ausarbeitung mündlicher Prüfungsfragen

Vorwort

Diese Ausarbeitung dient dem einfacheren und übersichtlicheren Lernen. Es sei aber gesagt, dass es wahrscheinlich nicht ausreicht nur die Fragen hier zu lernen, da nicht alles vorkommt, was auch tatsächlich gefragt wird (obwohl die Überdeckungswahrscheinlichkeit schon eher so 90% ist schätze ich) und teilweise die Ausführungen an manchen Stellen zu kurz sind. Vor allem die späteren Kapitel (die fast immer gefragt werden): Analytische Statistik, varianzanalyse, Regression/Korrelation sollte auf jeden Fall in kooperation mit dem Skriptum oder anderen Resourcen gelernt werden.

Anmerkung: Dutter möchte meistens auch die grafische Darstellung von Parametern wissen. Konkretes Beispiel: Wo sieht man das $z_{1-{\frac {\alpha }{2}}}$ in der Normalverteilung?

Weiters sollten auch die wichtigsten Formeln auswendiggelernt werden (Teststatistiken, wie man die Parameter ausrechnet). Herleitungen werden nicht immer verlangt, geben aber sicher Bonsupunkte.

Versionen

Diese Ausarbeitung von Prüfungsfragen, die häufig zur mündlichen Prüfung kommen, wurde ursprünglich von michi204 ausgearbeitet (hier gepostet). Die Version, die dieser Version zugrunde liegt, wurde von dodlhuat weiter verbessert und hier gepostet. Neu strukturiert und Detail-erweitert von For3st (2009/08).

Beschreibende Statistik

Welche Momente einer Verteilung gibt es?

Siehe auch Kapitel 3.3, S. 25 ff..

1. Momente (Lageparameter)

• Der Mittelwert oder Erwartungswert ("arithmetische Mittel"): ${\bar {x}}={\frac {1}{n}}\cdot \sum _{i=1}^{n}x_{i}$
• Der Median ist der mittlere Wert einer geordneten Stichprobe bzw. das arithmetische Mittel der beiden mittleren Werte bzw. er ist das 50%-Quantil ( siehe Quantil).
• Der Modus oder Modalwert ist der häufigste Wert einer Verteilung. Sind mehrere Werte gleich häufig, wird die Mitte dieser Werte angenommen, falls die Werte nebeneinander liegen, ansonsten ist der Modalwert undefiniert.
• Bei einem $\alpha$-Quantil $Q_{\alpha }$ ist ein $\alpha$-Anteil der Verteilung kleiner oder gleich und ein ($1-\alpha$)-Anteil grösser oder gleich $Q_{\alpha }$. Der Wert der Verteilungsfunktion $F(x)$ ergibt also für das $\alpha$-Quantil genau $F(Q_{\alpha })=\alpha$.
• Ein Perzentil $P_{\alpha }$ ist analog, nur mit Prozentangaben, definiert.
• Quartile sind die .25- bzw. .75-Quantile (identisch mit den 25%- und 75%-Perzentilen).

2. Momente (Streuungsparameter)

• Die Varianz ist das mittlere Abstandsquadrat vom Mittelwert: $s^{2}={\frac {1}{n-1}}\cdot \sum (x_{i}-{\bar {x}})^{2}$.
• Die Standardabweichung oder Streuung ist die Wurzel der Varianz, also $s={\sqrt {s^{2}}}$. Eine "grobe Faustformel" für die Streuung ist ${\frac {Maximalwert-Minimalwert}{3}}$
• Der Interquartilabstand IQR $IQR=Q_{0,75}-Q_{0,25}$ ACHTUNG: $s_{IQR}={\frac {Q_{0,75}-Q_{0,25}}{1,349}}$ ist die approximierte Standardabweichung durch den IQR. Das ist nicht der IQR selber.
• Der Median der absoluten Abweichung vom Median Medmed $s_{Medmed}={\frac {1}{0,6745}}\cdot med(|x_{i}-median|)$

3. Moment (Schiefe)

Die Schiefe ist grösser als Null wenn es mehr positive als negative Abweichungen vom Mittelwert gibt:

${\frac {{\frac {1}{n}}\cdot \sum (x_{i}-{\bar {x}})^{3}}{s^{3}}}$

4. Moment (Kurtosis)

Kurtosis mit unterschiedlichen Parametern. flache Wölbung: negative Kurtosis, spitze Wölbung: positive Kurtosis

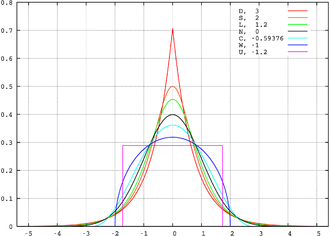
Die Kurtosis (auch Wölbung oder Exzess) wird auch "heavy tails" genannt, sie ist ein Maß für die "Flachheit einer Verteilung".

${\frac {{\frac {1}{n}}\cdot \sum (x_{i}-{\bar {x}})^{4}}{s^{4}}}-3$

Bei Schiefe und Kurtosis hat es sich eingebürgert, einfach durch n zu dividieren. Durch das Subtrahieren von 3 hat die N(0,1)-Verteilung eine Kurtosis von 0.

Was ist das Messniveau? Welche Skalen gibt es, was charakterisiert sie, welche Momente sind dort verwendbar?

Das Messniveau gibt eine Unterteilung in verschiedene Datentypen / Skalen vor:

Nominalskala

z.B. Geschlecht: keine Ordnung, Modalwert

Ordinalskala

z.B. Schulnoten: Ordnung, aber keine Abstände: Modalwert, Median, Quantile

Intervallskala

z.B. Temperatur °C: Ordnung, Abstände, kein abs. Nullpunkt: Modalwert, Median, Quantile, Mittel

Verhältnisskala

z.B. Temperatur in Kelvin: Ordnung, Abstände, absoluter Nullpunkt: Modalwert, Median, Quantile, Mittel

Was ist der MedMed?

Der MedMed, oder kurz MAD (Median Absolute Deviation) ist ein robustes Streuungsmaß. Es wird berechnet, indem man den Median berechnet und dann alle Abweichungen der Datenwerte von Median berechnet. Diese Abweichungen sortiert man nun der Größe nach und wählt wieder den Median (daher auch der Name MedMed).

Achtung: Bei der Verwendung des MedMed gibt es einen Faktor zu berücksichtigen, damit der Wert des MAD mit der Standardabweichung vergleichbar ist! Ähnliches gilt beim durch den IQR (Inter-Quartil-Range) approximierte Standardabweichung $s_{IQR}$

Was ist die Varianz? Warum n-1 Freiheitsgrade?

Die Varianz ist ein Maß, das beschreibt, wie stark eine Messgröße (genauer eine Zufallsgröße) „streut“. Sie wird berechnet, indem man die Abstände der Messwerte vom Mittelwert quadriert, addiert und durch die Anzahl der Messwerte teilt.

Die Formel:

$s^{2}={\frac {1}{n-1}}\cdot \sum (x_{i}-{\bar {x}})^{2}$

(manchmal "korrigierte Stichprobenvarianz" oder "empirische Varianz" genannt, meist mit s² statt σ² dargestellt)

Man geht von n unabhängigen Stichprobenwerten aus, also n Freiheitsgraden. Da man jedoch die Differenz vom bereits bekannten Mittelwert bildet und die Summe aller Abweichungen 0 ist, kennt man bei n-1 Abweichungen bereits auch die letzte Abweichung, daher n-1 Freiheitsgrade. Ein nicht unerwünschter Nebeneffekt ist, das die Varianz nun für n=1 nicht definiert ist statt 0.

Video wo rechnerisch skizziert wird warum die Formel mit dem n-1 eine bessere Erwartungstreue hat: [1]

Wikipedia rechnet die Erwartungstreue auch vor.

Was ist die Standardabweichung?

Die Standardabweichung (oder Streuung) ist die mittlere Abweichung vom arithmetischen Mittel einer Verteilung. Sie berechnet sich aus der Quadratwurzel der Varianz und ist ein Streuungsmaß, gibt also die Breite der Verteilung an. Eine sehr grobe Schätzung für die Standardabweichung lautet: ${\frac {Maximalwert-Minimalwert}{3}}$

Wahrscheinlichkeitstheorie

(Elementar-)Ereignisse, Ereignisalgebra, Ereignisraum, Operationen, Borel-Mengen

Siehe auch Kapitel 4.1

Führt man einen Versuch (z.B. Würfeln mit 2 Würfeln) durch, kann dieser verschiedene Versuchsausgänge haben ((1,1), (1,2), … , (6,6)). Die Menge aller möglichen Versuchsausgänge heißt Ω (Stichprobenraum), und jede Teilmenge (z.B. 2 gleiche = {(1,1),(2,2), …, (6,6)} heißt Ereignis, einpunktige Teilmengen (z.B. (1,1)) heißen Elementarereignisse.

Auf Ereignisse kann man folgende Operationen anwenden:

• Durchschnittsbildung ("A und B": $A\cap B$)
• Vereinigung ("A oder B": $A\cup B$)
• Komplementbildung ("nicht A": $A^{c}$)

Besondere Ergeinisse:

• Das unmögliche Ereignis Ø zb: $A\cap A^{c}$
• Das sichere Ereignis Ω zb: $A\cup A^{c}$

Ereignisse können disjunkt sein (ihr Durchschnitt ist leer). Ein Ereignis A kann ein anderes B implizieren ($A\subset B$), dh A ist in B enthalten. Eine Reihe von Ereignissen ist genau dann Zerlegung eines anderen Ereignisses, wenn ihre Vereinigung das andere Ereignis ergibt und sie alle disjunkt sind. Die Regeln von De Morgan gilt daher:

$A\cap B=(A^{c}\cup B^{c})^{c}$

und

$A\cup B=(A^{c}\cap B^{c})^{c}$.

Die Menge aller betrachteten Ereignisse daher die Menge aller Teilmengen von Ω heißt Ereignisraum A (z.B. $\{\{(1,1)\},\{1,1\}\cup \{1,2\},\dots \}$). Zusammen mit den Operationen (Durchschnitt, Vereinigung, Komplementbildung), dem sicheren Ereignis Ω und Ø (unmögliches Ereignis) heißt der Ereignisraum Ereignisalgebra. Ist diese bezüglich Vereinigung und Komplementbildung abgeschlossen, heißt sie Ereignis-σ-Algebra.

Ist die Menge aller möglichen Versuchsausgänge $\mathbb {R}$, und nimmt man als Ereignisalgebra die Menge aller links halboffenen Intervalle sowie Vereinigungen und Komplemente dieser, dann ist die kleinste σ-Algebra, die all diese Mengen enthält, die borelsche σ-Algebra B, Teilmengen davon Borel-Mengen.

Welche Arten von Wahrscheinlichkeiten gibt es?

Während die a-priori-Wahrscheinlichkeit theoretischer Natur ist und im Vorhinein angegeben wird (Münze hat 2 gleich wahrscheinliche Seiten, daher $P(W)={\tfrac {1}{2}}$), bestimmt man die a-posteriori-Wahrscheinlichkeit empirisch (57 von 100 Münzwürfen haben Wappen gezeigt, daraus folgt: $P(W)={\tfrac {57}{100}}$).

Was ist ein Wahrscheinlichkeitsmaß?

Siehe auch Kapitel 4.2 (S. 39).

Ein Maß μ weist jedem Elementarereignis aus Ω und damit jedem Ereignis aus A ein Gewicht zu, ist also eine Funktion vom Ereignisraum A in $[0,\infty ]$. Für Maße gilt natürlich σ- Additivität, dh die Summe aller Maße einer Zerlegung eines Ereignisses ergibt das Maß dieses Ereignisses. Gilt auch μ(Ω) = 1, hat man ein Wahrscheinlichkeitsmaß, und man schreibt fortan P statt μ. Die Wahrscheinlichkeit eines Ereignisses ist dann die Summe der Wahrscheinlichkeiten seiner Elementarereignisse. Sind alle Gewichte gleich, ist die Wahrscheinlichkeit eines Ereignisses gleich der Anzahl der günstigen dividiert durch die Anzahl der möglichen Elementarereignisse.

Rechenregeln:

$P(A)=1-P(A^{c})$

$P(A-B)=P(A)-P(A\cap B)$

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Was ist ein Wahrscheinlichkeitsraum?

Die Menge aller möglichen Versuchsausgänge Ω zusammen mit der darauf definierten σ-Algebra ${\mathfrak {A}}$

Was ist eine bedingte Wahrscheinlichkeit? Was bedeutet Unabhängigkeit von Ereignissen?

Durch das Vorwissen wird der Ereignisraum eingeschränkt, sodass die Wahrscheinlichkeiten sich ändern (z.B. 1 Würfel mit den Ereignissen A: "Zahl≤3" und B: "Zahl=1". Dann ist $P(B)={\tfrac {1}{6}}$, aber es gilt $P(B|A)={\tfrac {1}{3}}$).

Es gilt: $P(B|A)={\tfrac {P(B\cap A)}{P(A)}}$, also die Wahrscheinlichkeit für A und B, normiert auf den durch den Eintritt von A bereits eingeschränkten Ereignisraum. Wenn der Eintritt von A keinen Einfluss mehr hat, daher P(B|A) = P(B), nennt man die Ereignisse A und B unabhängig. Aus obiger Formel erhält man: $P(B\cap A)=P(B|A)\cdot P(A)$. Für unabhängige Ereignisse gilt dann wegen $P(B|A)=P(B)$ -> $P(B\cap A)=P(B)\cdot P(A)$.

Was ist eine Zufallsvariable? Wann ist sie diskret/kontinuierlich? Was ist eine Dichtefunktion? Was ist eine Verteilungsfunktion? Transformationen von Zufallsvariablen?

Eine Zufallsvariable ist formal eine Abbildung von einem Wahrscheinlichkeitsraum $(\Omega ,{\mathfrak {A}},P)$ in einen einfacheren $(\Omega ,{\mathfrak {B}},P_{1})$. Jede Menge B aus ${\mathfrak {B}}$ muss ein Urbild $A=X^{-1}(B)$ besitzen.

Eine diskrete Zufallsvariable kann höchstens abzählbar viele verschiedene Werte annehmen. $p_{i}=P(X=x_{i})$ gibt eine Punktwahrscheinlichkeit an und heißt Wahrscheinlichkeitsfunktion, und es gilt $\sum _{i=1}^{n}p_{i}=1$.

$F(x)=P(X\leq x)$ ist gleich der Summe über $p_{i}$ bis x und heißt Verteilungsfunktion.

Eine Zufallsvariable ist stetig, wenn es eine nicht negative Funktion f(x) gibt ,sodass sich die Verteilungsfunktion F(x) für alle $x\ \epsilon \ \mathbb {R}$ als Integral über f darstellen lässt.

Die Verteilungsfunktion $F(x)=P(X\leq x)$ ist gleich dem Integral über f von $-\infty \ bis\ x$. f heißt Dichtefunktion und ist die Ableitung der Verteilungsfunktion.

Transformationen von Zufallsvariablen: Addition wirkt sich nur auf den Mittelwert aus (verschiebt sich um addierten Betrag), Multiplikation wirkt sich auf die Varianz aus (diese wird dividiert). Zieht man den Mittelwert einer normalverteilten Zufallsvariablen ab und dividiert durch die Standardabweichung, erhält man eine N(0,1), also standard-normalverteilte Zufallsvariable.

Was ist ein Wahrscheinlichkeitsnetz?

Im Wahrscheinlichkeitsnetz trägt man die Werte einer geordneten Stichprobe sowie die empirische Verteilungsfunktion auf. Bei Normalverteilung ergibt sich durch die Anordnung der y-Achse annähernd eine Gerade. Aus der Ausgleichsgeraden lassen sich die Parameter der Verteilung grafisch schätzen. bei 50%$\mu$ und bei 84,13% s

http://de.wikipedia.org/wiki/Empirische_Verteilungsfunktion

Was ist die mathematische Erwartung und die Varianz einer Zufallsvariablen?

Die Erwartung (oder der Mittelwert) einer Zufallsvariablen X ist im stetigen Fall das Integral der Dichtefunktion mal h(x)=x:

$E(X)=\int \limits _{-\infty }^{\infty }x\cdot f(x)dx$

und im diskreten Fall:

$E(X)=\sum _{i=1}^{n}x_{i}\cdot p_{i}$

Die Varianz einer Zufallsvariablen X ist:

$Var(X)=E(X^{2})-(E(X))^{2}$

Dutter ist hier lieber die nicht ausmultiplizierte Form zu verwenden: $Var(X)=E[X-E(X)]^{2}$

Die Standardabweichung einer Zufallsvariablen ist $\sigma ={\sqrt {Var(X)}}$.

Was ist eine mehrdimensionale (multivariate) Zufallsvariable? Was ist eine Randverteilung? Wann sind zwei Zufallsvariablen voneinander unabhängig?

Siehe auch Kapitel 4.5, S. 60 ff..

In der Praxis wird selten eine Größe alleine untersucht, da die Zusammenhänge zwischen verschiedenen Merkmalen wichtig sind. Man kann nun einen p-dimensionalen Zufallsvektor $(X_{1},...,X_{p})$ definieren. Verteilungsfunktion und Wahrscheinlichkeitsdichte können ähnlich wie im eindimensionalen Fall definiert werden.

Die Verteilung einer Zufallsvariablen unabhängig vom Wert der anderen (d.h. für alle Werte der anderen) heißt Randverteilung (Kapitel 4.5.1, S. 64).

Zwei Zufallsvariablen X und Y sind genau dann voneinander unabhängig, wenn die Verteilungsfunktion des Zufallsvektors $(X,Y)$ gleich dem Produkt der beiden Randverteilungsfunktionen ist, daher:

$F(x,y)=F_{X}(x)*F_{Y}(y)\quad \forall x,y\in \mathbb {R}$.

Die Randverteilung sieht folgendermaßen aus:

im diskreten [2] Fall

$X:p_{i.}=P_{X,i}=P(X=x_{i})=\sum _{j=1}^{\infty }p_{ij}$
bzw.
$Y:p_{.j}=P_{Y,i}=P(Y=y_{j})=\sum _{i=1}^{\infty }p_{ij}$

im stetigen Fall

$f_{X}(x)=\int \limits _{-\infty }^{\infty }f(x,y)dy$
bzw.
$f_{Y}(y)=\int \limits _{-\infty }^{\infty }f(x,y)dx$

Y/X	0	1	2	3	$P(Y=j)=p_{.j}$
1	$0$	${\tfrac {3}{8}}$	${\tfrac {3}{8}}$	$0$	${\tfrac {6}{8}}$
3	${\tfrac {1}{8}}$	$0$	$0$	${\tfrac {1}{8}}$	${\tfrac {2}{8}}$
$p_{i.}=P(X=i)$	${\tfrac {1}{8}}$	${\tfrac {3}{8}}$	${\tfrac {3}{8}}$	${\tfrac {1}{8}}$	$1$

Was besagt der zentrale Grenzwertsatz?

Besitzt die Verteilung der Grundgesamtheit eine endliche Varianz, was meist der Fall ist, so ist die Verteilung der arithmetischen Mittel von Zufallsstichproben für einen genügend großen Stichprobenumfang annähernd normalverteilt.

Analytische Statistik

Was ist eine Stichprobe?

Eine Untermenge einer Population heißt Stichprobe. Mathematisch gesehen stellt sie einen n-dimensionalen Zufallsvektor $(X_{1},\dots ,X_{n})$ mit unabhängig und identisch verteilten Elementen $X_{i}$ dar. Die Stichprobenwerte $(x_{1},\dots ,x_{n})$ sind eine Realisation dieses Zufallsvektors. Damit mit einfachen Mitteln Aussagen über die Verteilung oder ihre Parameter gemacht werden können, müssen die Stichprobenwerte zufällig aus der Population gewählt werden.

Was ist ein Schätzer? Wann ist er erwartungstreu, konsistent, oder effizient?

Ein Schätzer 't' (auch eine Schätzfunktion genannt, siehe auch Skriptum Kap. 5.2, S. 76) berechnet einen Parameter q einer Verteilung näherungsweise aus Stichprobenwerten:

${\hat {\theta }}=t(x_{1},\dots ,x_{n})$

Eine Funktion der Stichprobe wird allgemein als Statistik bezeichnet (und ist auch eine Zufallsvariable). Im Falle der Verwendung zur näherungsweisen Bestimmung (Schätzung) gewisser Kenngrößen spricht man von einem Schätzer. Eine Realisation eines Schätzers heißt Schätzwert oder Schätzung.

Eine Schätzfunktion heißt erwartungstreu, wenn der Erwartungswert der Schätzfunktion den geschätzten Parameter ergibt.

Eine Schätzfunktion heißt konsistent, wenn sie sich mit wachsendem n (größerer Stichprobe) immer mehr dem geschätzten Parameter nähert, d. h. ihre Varianz kleiner wird.

Ein Schätzer ist dann effizient, wenn er die kleinstmögliche Varianz aufweist.

Wenn die Verteilung symetrisch ist, stellt der Median ${\tilde {X}}$ ebenfalls einen konsistenten und erwartungstreuen Schätzer der Erwartung dar. Die Güte des Schätzers hängt von seiner Variabilität ab, d.h. je kleiner die Varianz desto besser. (1/3 mehr Beobachtungen für ${\tilde {X}}$ um die gleiche Genauigkeit wie bei ${\bar {X}}$ zu erhalten)

siehe http://www.statistik.tuwien.ac.at/public/dutt/vorles/inf_bak/node46.html

Was macht die likelihood-Funktion? Was ist die Maximum-Likelihood-Methode?

Die Maximum-Likelihood-Methode soll einen brauchbaren Schätzer für Parameter einer Verteilung finden, indem sie jenen Wert des Parameters wählt, der die Stichprobe als wahrscheinlichstes Resultat erscheinen lässt. Dazu wird der Parameter θ so gewählt, dass die Likelihood-Funktion $l(\theta ;x_{1},\dots ,x_{n})=f_{\theta }(x_{1})\cdot \dots \cdot f_{\theta }(x_{n})$ ein Maximum annimmt ($f$ ist die Dichtefunktion der Verteilung).

Was ist ein Konfidenzintervall?

Ein $(1-\alpha )$-Konfidenzintervall für einen Parameter ist ein Intervall um den geschätzten Parameter, in dem der tatsächliche Parameter mit der Überdeckungswahrscheinlichkeit $1-\alpha$ liegt. $\alpha$ heißt dabei Konfidenzzahl.

Konfidenzintervall für den Mittelwert

Das Konfidenzintervall (siehe auch Kapitel 5.3, S. 79). Zugrunde liegt die Tatsache, dass der Mittelwert ${\bar {X}}$ einer Normalverteilung $N(\mu ,\sigma ^{2})$ selbst einer Normalverteilung $N(\mu ,{\tfrac {\sigma ^{2}}{n}})$ unterliegt. Nun wird diese Verteilung so transformiert, dass daraus eine $N(0,1)$- Verteilung, also eine Standardnormalverteilung, wird. Die Transformation ist nun ${\tfrac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}$. Wichtig ist zu erkennen, dass durch diese Transformation tatsächlich aus der $N(\mu ,{\tfrac {\sigma ^{2}}{n}})$-Verteilung für ${\bar {X}}$ eine $N(0,1)$-Verteilung wird. Gemäß den Transformationsregeln (S. 29) ergibt die Transformation ${\tfrac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}={\tfrac {1}{\sigma /{\sqrt {n}}}}\cdot {\bar {X}}-{\tfrac {\mu }{\sigma /{\sqrt {n}}}}$ den Mittelwert

$y_{\mu }=ax_{\mu }+b={\tfrac {1}{\sigma /{\sqrt {n}}}}\cdot \mu -{\tfrac {\mu }{\sigma /{\sqrt {n}}}}=0$

und die Varianz (wobei $s_{x}^{2}={\tfrac {\sigma ^{2}}{n}}$)

$s_{y}^{2}=a^{2}s_{x}^{2}=\left({\tfrac {1}{\sigma /{\sqrt {n}}}}\right)^{2}\cdot s_{x}^{2}={\tfrac {1}{\sigma ^{2}/n}}\cdot s_{x}^{2}={\tfrac {n}{\sigma ^{2}}}\cdot {\tfrac {\sigma ^{2}}{n}}=1$

Die Wahrscheinlichkeit, dass der transformierte Mittelwert (der nun standard-normalverteilt ist) nun in den entsprechenden Bereich fällt, entspricht dem $\alpha$-Quantil der Standard-normalverteilung. Es gilt daher:

${\bigg (}z_{\tfrac {\alpha }{2}}<{\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}<z_{1-{\tfrac {\alpha }{2}}}{\bigg )}$.

Wenn die beiden Ungleichungen ausgerechnet werden, ergibt sich die Formel fuer das Konfidenzintervall:

${\bigg (}{\bar {x}}-z_{1-{\tfrac {\alpha }{2}}}\cdot {\frac {\sigma }{\sqrt {n}}},{\bar {x}}+z_{1-{\tfrac {\alpha }{2}}}\cdot {\frac {\sigma }{\sqrt {n}}}{\bigg )}$

Ist die Standardabweichung unbekannt, wird das Konfidenzintervall länger, da es aus der Stichprobe geschätzt werden muss. Aus der Standard-Normalverteilung wird dann magisch eine Student-t-Verteilung mit n-1 Freiheitsgraden (Warum?). Das Konfidenzintervall sieht dann so aus:

${\bigg (}{\bar {x}}-t_{n-1;1-{\tfrac {\alpha }{2}}}\cdot {\frac {S}{\sqrt {n}}},{\bar {x}}+t_{n-1;1-{\tfrac {\alpha }{2}}}\cdot {\frac {S}{\sqrt {n}}}{\bigg )}$

Die t-Verteilung entspricht im Prinzip einer Normalverteilung bei kleinem n, d.h. mit weniger Stichproben. Ab n>30 ist die t-Verteilung durch die N-Verteilung annäherbar. Da ich in der N-Verteilung die Stichprobenanzahl nirgends unterbringen kann, sattel ich in diesem Fall auf die t-Verteilung um und kann statt der Varianz (die ich ja gar nicht weiß) die Stichprobenzahl in Form der Freiheitsgrade hinein bringen. Wenn die Stichprobenzahl groß genug ist, nähert sich die t-Verteilung eh der N-Verteilung an, wenn sie aber eigentlich zu klein ist, dann hab ich mit der t-Verteilung ein viel seriöseres Intervall, das breiter ist, weil ich weniger Informationen habe.

Intervallsschätzung mit $\mu$ bei unbekannten $\sigma$ (1-Stichproben-t-Test)

TODO: Herleitung laut Skriptum (Kapitel Intervallsschätzungen -> mit $\mu$ bei unbekannten $\sigma$)

Hypothesen:

$H_{0}:\mu =\mu _{0},\qquad H_{1}:\mu >\mu _{0}$

Teststatistik:

$T=\mu _{0}+{\frac {S}{\sqrt {n}}}\cdot t_{n-1;1-\alpha }$

Kritischer Bereich:

${\bar {X}}>T$

Konfidenzintervall für die Varianz

Konfidenzintervall für $\sigma ^{2}$ (siehe auch Kapitel 5.8.1, S. 97)

${\Bigg (}{\frac {(n-1)\cdot S^{2}}{\chi _{n-1;1-{\tfrac {\alpha }{2}}}^{2}}},{\frac {(n-1)\cdot S^{2}}{\chi _{n-1;{\tfrac {\alpha }{2}}}^{2}}}{\Bigg )}$

Was ist eine Hypothese? Was ist die Nullhypothese, was die Alternative? Fehler 1./2. Art?

Zusatzinfo: [3]

Hypothesen

Unter Hypothese versteht man in der Statistik eine anhand empirischer Daten zu prüfende Annahme.

Eine Nullhypothese ($H_{0}$) ist eine Annahme (z.B. über die Verteilung einer Zufallsvariablen oder den Wert eines Parameters), die getestet werden soll.

Die Alternativhypothese ($H_{1}$) steht für eine Menge von alternativen Annahmen bezüglich der Nullhypothese. Falls die Nullhypothese nicht verworfen werden kann, besteht aus statistischer Sicht allerdings kein Grund, von ihrer Gültigkeit auszugehen (vgl. Fehler 2. Art).

Die Teststatistik ist eine nach einer bestimmten Vorschrift berechnete Zufallsvariable. Fällt der Wert der Teststatistik in den so genannten kritischen Bereich, wird die Nullhypothese verworfen und $H_{1}$ angenommen.

Fehlerwahrscheinlichkeiten

Die Fehlerwahrscheinlichkeit 1. Art ("$\alpha$-Fehler") gibt die Wahrscheinlichkeit an, dass die richtige Hypothese abgelehnt wird ("false positive"). Er passiert mit der Wahrscheinlichkeit $\alpha$ (=Signifikanzniveau). Die Fehlerwahrscheinlichkeit 2. Art ("$\beta$-Fehler") gibt die Wahrscheinlichkeit an, dass eine falsche Hypothese als richtig angenommen wird ("false negative"). Die Fehlerwahrscheinlichkeiten können durch Vergrößern des Stichprobenumfangs verkleinert werden. Die Wahrscheinlichkeit, mit der eine falsche Nullhypothese entlarvt wird, heißt Macht oder Schärfe eines Tests und kann mit $1-\beta$ angegeben werden. Anders gesagt: Wenn man in einer Verteilung sich jeweils das $\beta$ ausrechnet und die 1- $\beta$ Werte in einer Kurve aufträgt, kann man in der Kurve die Macht ablesen.

Siehe auch Kapitel 5.5, S. 87 und Hypothese@Wikipedia

2 Populationen

Vergleich der Mittel (2-Stichproben-t-Test) (Spezialfall der Varianzenanalyse)

Man vergleicht damit die Mittel zweier Populationen untereinander (2-Stichproben-t-Test) oder man vergleicht das Mittel einer Population mit einem vorgegebenen Wert (1-Stichproben-t-Test, nur bei unbekannter Standardabweichung).

Hypothesen:

$H_{0}:\mu _{x}=\mu _{y},\qquad H_{1}:\mu _{x}\neq \mu _{y}$

Teststatistik:

$T={\frac {{\bar {X}}-{\bar {Y}}}{\sqrt {{\frac {(n_{1}-1)s_{x}^{2}+(n_{2}-1)s_{y}^{2}}{n_{1}+n_{2}-2}}\cdot ({\frac {1}{n_{1}}}+{\frac {1}{n_{2}}})}}}={\sqrt {\frac {n_{1}n_{2}(n_{1}+n_{2}-2)}{n_{1}+n_{2}}}}\cdot {\frac {{\bar {X}}-{\bar {Y}}}{\sqrt {(n_{1}-1)s_{x}^{2}+(n_{2}-1)s_{y}^{2}}}}$

Kritischer Bereich:

$-t_{n_{1}+n_{2}-2;1-{\tfrac {\alpha }{2}}}<T<t_{n_{1}+n_{2}-2;1-{\tfrac {\alpha }{2}}}$

Vergleich der Varianzen

Mit Hilfe des F-Tests:

$H_{0}:\sigma _{x}^{2}=\sigma _{y}^{2}\qquad H_{1}:\sigma _{x}^{2}>\sigma _{y}^{2}$

Teststatistik:

$T={\frac {s_{x}^{2}}{s_{y}^{2}}}$

Kritischer Bereich:

$T>F_{n_{1}-1,n_{2}-1,1-\alpha }$

Anpassungstests

Wozu dient der $\chi ^{2}$-Anpassungstest?

Mit Hilfe dieses Tests kann man eine Hypothese über die Form einer Verteilung prüfen. Dazu teilt man die Stichprobe in k Klassen ein und berechnet die Teststatistik:

$T=\sum _{i=1}^{k}{\frac {(h_{i}-e_{i})^{2}}{e_{i}}}$

$e_{i}=p_{i}\cdot n$

wobei $h_{i}$ die Häufigkeiten und $e_{i}$ die theoretischen Wahrscheinlichkeiten (aufgrund der mit $H_{0}$ angenommenen Verteilung) $p_{i}$ multipliziert mit $n$ sind.

Als kritischen Bereich nimmt man:

$T>\chi _{k-1;1-\alpha }^{2}$

Wozu dient der Kolmogorov-Smirnov-Test?

Man testet damit ob zwei Zufallsvariablen die selbe Verteilung haben oder ob einer Zufallsvariable eine hypothetische Verteilung $F_{0}$ zugrunde liegt, indem man die absolute Differenz zwischen empirischer und hypothetischer Verteilungsfunktion betrachtet.

Varianzanalyse

Was geschieht bei der Varianzanalyse? Was steht in der Varianzanalyse-Tafel?

Eine betrachtete Größe weist oft eine Variation auf, die sich aus zufälliger Variation sowie Variation durch einen bestimmten Einfluss zusammensetzt. In der Varianzanalyse trennt man diese beiden Variationen (Varianzzerlegung). Dazu wird die Quadratsumme (Summe der Abweichungen vom Stichprobenmittel) zerlegt.

Mit Hilfe der Varianzanalyse kann man die Mittelwerte von k Normalverteilungen vergleichen. Man nimmt $H_{0}:\mu _{1}=\mu _{2}=\dots =\mu _{k}$ gegen $H_{1}:\mu _{r}\neq \mu _{s}$ für mindestens ein $r\neq s$. Danach berechnet man die Quadratsumme innerhalb jeder Stichprobe $q_{I}$ und die Quadratsumme zwischen den Stichproben $q_{Z}$:

$q_{I}=\sum _{j=1}^{k}\sum _{i=1}^{n_{j}}(x_{ij}-{\bar {x}}_{j})^{2}=\sum _{j=1}^{k}(n-1)\cdot s_{x_{j}}^{2}$ $q_{Z}=\sum _{j=1}^{k}n_{j}({\bar {x}}_{j}-{\bar {x}})^{2}$

Die Varianzanalyse-Tabelle sieht so aus:

Variation	Freiheitsgrade FG	Quadratsumme q	mittlere Quadratsumme $s^{2}$	F
Zwischen den Gruppen	k-1	$q_{Z}$	$s_{Z}^{2}={\frac {q_{Z}}{k-1}}$	${\frac {(n-k)\cdot q_{Z}}{(k-1)\cdot q_{I}}}$
Innerhalb der Gruppe	n-k	$q_{I}$	$s_{I}^{2}={\frac {q_{I}}{n-k}}$
Total	n-1	q

Der Wert der Teststatistik F wird nun gegen den kritischen Bereich getestet:

$H_{0}:\mu _{1}=\mu _{2}=\dots =\mu _{k},\qquad H_{1}:\mu _{r}\neq \mu _{s}$ für mindestens ein $r\neq s$

Teststatistik:

$F={\frac {q_{Z}/(k-1)}{q_{I}/(n-k)}}={\frac {(n-k)\cdot q_{Z}}{(k-1)\cdot q_{I}}}$

Kritischer Bereich:

$F>F_{k-1;n-k;1-\alpha }$

Regression und Korrelation

Was ist Regression? Was ist das Regressionsproblem? Regressionsgerade? Residuen? Wie testet man auf Abhängigkeit einer Variablen x?

Das Regressionsproblem behandelt die Verteilung einer Variablen Y, wenn (mindestens) eine andere Variable x nicht zufällige Werte annimmt. x heißt unabhängig und ist keine Zufallsvariable. Y ist eine Zufallsvariable und abhängig von x, sofern eine Regression vorliegt. Für jeden gewählten Wert von x gibt es eine Verteilung von Y mit einem Mittelwert $\mu _{y.x}$ und einer Varianz $\sigma _{y.x}^{2}$. Liegt eine einfache, lineare Regression vor, so kann die Abhängigkeit der Mittelwerte $\mu _{y.x}$ von Y durch die Regressionsgerade angegeben werden:

${\hat {y}}_{x}={\hat {a}}+{\hat {b}}(x-{\bar {x}})$

Die Parameter der Regressionsgeraden ${\hat {a}}$ und ${\hat {b}}$ werden aus den Stichprobenwerten geschätzt, wobei man für ${\hat {a}}$ den Wert ${\bar {y}}$ und für ${\hat {b}}$ den Quotienten ${\tfrac {s_{xy}}{s_{x}^{2}}}$ verwendet. $s_{x}^{2}$ ist dabei die empirische Varianz der unabhängigen Variable und errechnet sich daher aus:

$s_{x}^{2}={\frac {1}{n-1}}\cdot \sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}$

Die empirische Kovarianz $s_{xy}$ ergibt sich aus der Summe aller Produkte von Mittelabweichungen beider Variablen dividiert durch n-1 Freiheitsgrade:

$s_{xy}={\frac {1}{n-1}}\cdot \sum _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})={\frac {1}{n-1}}{\Big (}\sum (x_{i}y_{i})-n{\bar {x}}{\bar {y}}{\Big )}$

Auch die Varianz der Beobachtungen $s^{2}$ kann geschätzt werden durch:

$s^{2}={\frac {1}{n-2}}\cdot \sum _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}={\frac {n-1}{n-2}}(s_{y}^{2}-{\hat {b}}^{2}s_{x}^{2})$

Die Differenzen zwischen gemessenen und geschätzten Werten $y_{i}-{\hat {y_{i}}}$ nennt man auch Residuen. Die Gerade wird so gewählt, dass die Summe der quadrierten Residuen minimal wird.

Nimmt man die Verteilung von Y für jedes x als normal an, kann man Konfidenzintervalle für die Parameter a, b, $\sigma ^{2}$ und $\mu _{y.x}$ angeben (mit Hilfe der Parameterschätzungen und der t-Verteilung, siehe Kapitel 7.3.1, S. 114).

Test auf Regression (Test auf Abhängigkeit)

Die Nullhypothese $H_{0}:b=0$ besagt, dass alle Mittelwerte von Y gleich sind (Alternative $H_{1}:b\neq 0$) und daher keine Regression vorliegt. Als Teststatistik verwendet man:

$T={\frac {{\hat {b}}\cdot s_{x}\cdot {\sqrt {n-1}}}{S}}={\hat {b}}\cdot {\sqrt {\frac {s_{x}^{2}\cdot (n-1)}{s^{2}}}}$

und der kritische Bereich ist:

$|T|>t_{n-2;1-{\tfrac {\alpha }{2}}}$,

Da der hier der Betrag $|T|$ angegeben ist, handelt es sich eigentlich um einen zweiseitig begrenzten Bereich, daher ist $1-{\tfrac {\alpha }{2}}$ zu nehmen.

Was ist Korrelation? Was ist das Korrelationsproblem? Was sind Kovarianz, empirische Kovarianz und Korrelationskoeffizient? Wie testet man auf Unkorreliertheit?

Das Korrelationsproblem behandelt die Frage, ob Korrelation vorliegt. Dies ist der Fall, wenn es einen Zusammenhang zwischen den Verteilungen zweier Zufallsvariablen X und Y gibt. Es wird also die gemeinsame Verteilung von X und Y betrachtet, ohne eine Variable zu fixieren. Oft geht man in solchen Problemen von einer bivariaten Normalverteilung aus. Für jedes X gibt es eine Verteilung von Y und umgekehrt.

Die Korrelation ρ zwischen X und Y ergibt sich aus der Kovarianz $\sigma _{XY}$ dividiert durch das Produkt der beiden Standardabweichungen $\sigma _{X}$ und $\sigma _{Y}$ und ist eine dimensionslose Größe im Intervall (–1,1); bei ρ = 0 sind X und Y unabhängig.

Als Schätzung verwendet man den empirischen Korrelationskoeffizienten, welcher sich wiederum aus der empirischen Kovarianz $s_{XY}$, dividiert durch das Produkt der empirischen Standardabweichungen $s_{X}$ und $s_{Y}$ berechnet:

$\rho _{XY}={\frac {\sigma _{XY}}{\sigma _{X}\cdot \sigma _{Y}}}\qquad r_{XY}={\frac {s_{XY}}{s_{X}\cdot s_{Y}}}$

Test auf Unkorreliertheit

Für den Test auf Unkorreliertheit (Test auf Unabhängigkeit, siehe auch S. 118) sind $H_{0}:\rho =0$ und $H_{1}:\rho \neq 0$. Der kritische Bereich ist:

$|T|>t_{n-2;1-{\frac {\alpha }{2}}}$

und als Teststatistik verwendet man:

$T=R\cdot {\sqrt {\frac {n-2}{1-R^{2}}}}$

wobei R die Zufallsvariable bezeichnet, die die Werte des empirischen Korrelationskoeffizienten $r_{XY}$ annimmt.

Was ist die Kovarianz ?

(Folgendes ist aus Wikipedia kopiert:)

Die Kovarianz ist in der Statistik eine (nichtstandardisierte) Maßzahl für den Zusammenhang zweier statistischer Merkmale (im Folgenden X und Y).

$s_{xy}={\frac {1}{n-1}}\cdot \sum _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})={\frac {1}{n-1}}{\Big (}\sum (x_{i}y_{i})-n{\bar {x}}{\bar {y}}{\Big )}$

• Die Kovarianz ist positiv, wenn X und Y tendenziell einen gleichsinnigen linearen Zusammenhang besitzen, d. h. hohe Werte von X gehen mit hohen Werten von Y einher und niedrige mit niedrigen.
• Die Kovarianz ist hingegen negativ, wenn X und Y einen gegensinnigen linearen Zusammenhang aufweisen, d. h. hohe Werte der einen Zufallsvariablen gehen mit niedrigen Werten der anderen Zufallsvariablen einher.
• Ist das Ergebnis 0, so besteht kein Zusammenhang oder ein nicht linearer Zusammenhang z. B. eine U-förmige Beziehung zwischen den beiden Variablen X und Y.

Die Kovarianz gibt zwar die Richtung einer Beziehung zwischen zwei Variablen an, über die Stärke des Zusammenhangs wird aber keine Aussage getroffen. Dies liegt an der Abhängigkeit des Ergebnisses von den Maßeinheiten der beteiligten Variablen X und Y. Ist z. B. die Kovarianz zweier Variablen mit der Maßeinheit "Meter" 5,2 so ist die Kovarianz der gleichen Werte in der Maßeinheit "Zentimeter" 520. Die Kovarianz ist deshalb in ihrer "Rohform" als Maßzahl für den stochastischen Zusammenhang nur wenig anschaulich und auch schwer vergleichbar.

Beispiel des Korrelationskoevizienten bei Scatter-Plot: [4]

Zählstatistik

Was ist das Klassifizierungsproblem? Was ist eine Kontingenztafel? Einfache, Zweifache Klassifizierung ?

Oft möchte man Dinge zählen, die in bestimmte Kategorien fallen. Es gibt das einfache Klassifizierungsproblem (z.B. 4 Klassen für Aussehen von Erbsen nach Kreuzungsversuch) und das zweifache Klassifizierungsproblem (z.B. Haarfarbe und Augenfarbe). Man hat jeweils vorgegebene theoretische Häufigkeiten und untersucht, ob die Abweichungen der tatsächlichen Häufigkeiten von ersteren nur zufälliger Natur sind. Eine Tabelle, die die absoluten Häufigkeiten der Merkmale gemeinsam darstellt, heißt Kontingenztafel. Teststatistik: $T=\sum {\frac {(h_{i}-e_{i})^{2}}{e_{i}}}$.

Der kritische Bereich ist eine $\chi ^{2}$-Statistik mit k-1 Freiheitsgraden im einfachen und (r-1)(c-1) Freiheitsgraden im zweifachen Fall.

Die Kontingenztafel sieht im einfachen Fall so aus (siehe auch Kapitel 8.1, S. 119):

Klassen	beobachtet	theoretisch	$h_{j}-e_{j}$	${\tfrac {(h_{j}-e_{j})^{2}}{e_{j}}}$
Klasse 1	$h_{1}$	$e_{1}$	$\ldots$	$\ldots$
Klasse 2	$h_{2}$	$e_{2}$	$\ldots$	$\ldots$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
Klasse k	$h_{k}$	$e_{k}$	$\ldots$	$\ldots$
Total	$h_{1}+\dots +h_{k}$	$e_{1}+\dots +e_{k}$	$\ldots$	$\ldots$

$T>\chi _{k-1;1-\alpha }^{2}$

Und beim Problem der zweifachen Klassifizierung ist das ganze naturgemäß umfangreicher. In der nachfolgenden Tabelle gibt es r Klassen für Merkmal A und c Klassen fuer Merkmal B. Die Einzelnen Zellen geben jeweils die tatsächlich auftretende Häufigkeit ($h_{..}$) und in Klammer die erwartete Häufigkeit ($e_{..}$) an:

	Merkmal B
Merkmal A	$B_{1}$	$B_{2}$	$\ldots$	$B_{c}$	$\sum$
$A_{1}$	$h_{11}({\hat {e}}_{11})$	$h_{12}({\hat {e}}_{12})$	$\ldots$	$h_{1c}({\hat {e}}_{1c})$	$h_{1.}$
$A_{2}$	$h_{21}({\hat {e}}_{21})$	$h_{22}({\hat {e}}_{22})$	$\ldots$	$h_{2c}({\hat {e}}_{2c})$	$h_{2.}$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$A_{r}$	$h_{r1}({\hat {e}}_{r1})$	$h_{r2}({\hat {e}}_{r2})$	$\ldots$	$h_{rc}({\hat {e}}_{rc})$	$h_{r.}$
$\sum$	$h_{.1}$	$h_{.2}$	$\ldots$	$h_{.c}$	$h_{..}=n$

$T=\sum {\frac {(h_{ij}-e_{ij})^{2}}{e_{ij}}}$

$T>\chi _{(r-1)\cdot (c-1);1-\alpha }^{2}$

Ein praktisches Beispiel kann in Kapitel 8.2, S. 120 bewundert werden.

Verteilungen

Im folgenden eine Zusammenfassung der wichtigsten Verteilungen. Vor allem Normalverteilung, Chi-Quadrat-, t- und F- Verteilung sollten gut gelernt werden (Dichtefunktion, etc.). Die Verteilungen sind in ungefährere absteigender Relevanz (für die Dutter Prüfung) geordnet. Nach der Erfahrung kann alles nach Binomialverteilung vernachlässigt werden (keine Gewähr).

Normalverteilung

Normalverteilungen mit unterschiedlichen Parametern

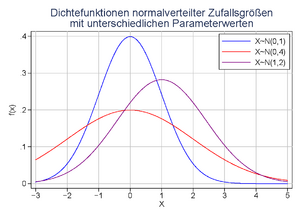
$N(\mu ,\sigma ^{2})$: kontinuierlich, symmetrisch.

Die Normalverteilung gilt zumindest annähernd für viele natürliche Prozesse. Aus dem Zentralen Grenzwertsatz folgt, dass aus vielen einzelnen unabhängigen Einflüssen entstehende Größen normalverteilt sind. Die Normalverteilung ist bei großem n eine gute Näherung für die Binomialverteilung.

Dichtefunktion: Gaußsche Glockenkurve mit arithmetischem Mittel der Verteilung als Höhepunkt, Mittel ± Standardabweichung als Wendepunkte.

Verteilungsfunktion: Anfang und Ende sehr flach und um den Median sehr steil.

$N(0,1)$ wird auch die Standardnormalverteilung genannt.

Chi-Quadrat-Verteilung

$\chi ^{2}$-Verteilungen mit unterschiedlichen Freiheitsgraden

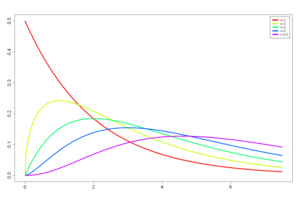
$\chi ^{2}(n)$: kontinuierlich, asymmetrisch. n ist der Freiheitsgrad.

Der Erwartungswert ist n, die Varianz 2n. Meist verwendet man die zentrale $\chi ^{2}$-Verteilung mit nur einem Parameter n. Die Summe quadrierter Zufallsvariablen (normalverteilt) ist $\chi ^{2}$-verteilt. Man verwendet diese Verteilung z.B. zur Schätzung der Varianz. Die $\chi ^{2}$-Verteilung ist sozusagen die quadrierte Normalverteilung.

Einige Verwendungszwecke:

• Anpassungstest
• Klassifizierungsproblem

Siehe auch die Chi-Quadrat-Verteilung auf der deutschen Wikipedia.

t-Verteilung

T-Verteilung mit ausgewählten Freiheitsgraden

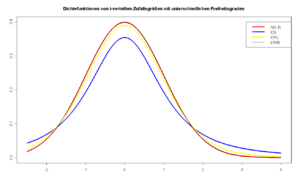
$t(m)$: kontinuierlich, symmetrisch. m sind Freiheitsgrade.

Erwartungswert: 0. Für große m (>30) kann die t-Verteilung durch die $N(0,1)$-Verteilung angenähert werden.

Die Varianz ergibt sich für $n>2$ als

$\operatorname {Var} (X)={\frac {n}{n-2}}.$

Einige Verwendungszwecke:

• Schätzung des Erwartungswertes bei unbekannter Varianz verwendet (statt der Standard-Normalverteilung bei bekannter Varianz), mit n-1 Freiheitsgraden
• Test auf Abhängigkeit (Regression), mit n-2 Freiheitsgraden
• Test auf Korrelation, mit n-2 Freiheitsgraden
• 1- und 2-Stichproben-t-Test, mit n-1 Freiheitsgraden

Siehe auch die Studentsche t-Verteilung auf der deutschen Wikipedia.

F-Verteilung

Dichtefunktion der F-Verteilung mit ausgewählten Freiheitsgraden m und n

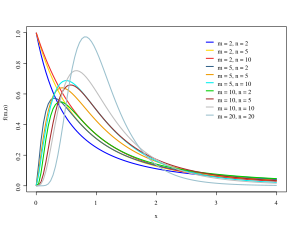
$F(m,n)$: kontinuierlich, asymmetrisch. m und n sind Freiheitsgrade.

Diese Verteilung ergibt sich aus dem Quotienten zweier $\chi ^{2}$ Verteilungen mit m bzw. n Freiheitsgraden:

$F(m,n)={\frac {\frac {\chi _{m}^{2}}{m}}{\frac {\chi _{n}^{2}}{n}}}$

Einige Verwendungszwecke:

• Test auf geiche Varianzen
• Varianzanalyse

Einige Bonusinformationen aus der Wikipedia:

Der Erwartungswert ist nur für $n>2$ definiert und lautet dann

$\operatorname {E} (X)={\frac {n}{n-2}}$.

Die Varianz ist nur für $n>4$ definiert und lautet dann

$\operatorname {Var} (X)={\frac {2n^{2}(m+n-2)}{m(n-2)^{2}(n-4)}}.$

Für manche Tests ist es nützlich zu wissen, dass gilt:

$F^{-1}(p;m;n)={\frac {1}{F^{-1}(1-p;n;m)}}$

Siehe auch die F-Verteilung auf der deutschen Wikipedia.

Binomialverteilung

$B(n,p)$: diskret, asymmetrisch.

Für p=0,5 symmetrisch.
$E(X)=np$
$Var(X)=np(1-p)$

Die Binomialverteilung kann zur Beschreibung von n Versuchen, die mit der Wahrscheinlichkeit p erfolgreich sind, verwendet werden. Für große n kann die Binomialverteilung gut durch die Normalverteilung angenähert werden.

$B(1,p)$ (daher mit nur einem Versuch) heißt auch Bernoulli-Verteilung.

Wie lässt sich die Binomialverteilung durch die Normalverteilung annähern?

Für große Werte von n lässt sich die Binomialverteilung durch die Normalverteilung mit dem Mittelwert $\mu =np$ und der Varianz $\sigma ^{2}=np(1-p)$ gut annähern. Für Werte von p nahe 0 oder 1 ist die Verteilung allerdings recht schief, für p nahe 0.5 ist die Annäherung recht gut.

Poissonverteilung

Poissonverteilung mit $\lambda =6$

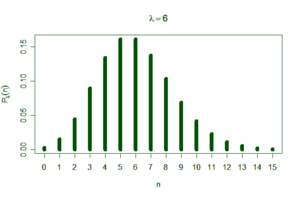
$P(\lambda )$: diskret, asymmetrisch.

λ ist zugleich Erwartungswert, Varianz und Schiefe. Für große $\lambda$ kann die Poisson-Verteilung durch die Normalverteilung mit $\mu =\lambda$ und $\sigma ^{2}=\lambda$ angenähert werden. Sie ist die Grenzverteilung der Binomialverteilung (für p → 0, n → ∞). Sie wird typischerweise für die Zahl von Phänomenen innerhalb einer Zeiteinheit verwendet.

Siehe auch die Poisson-Verteilung auf der deutschen Wikipedia.

Exponentialverteilung

Dichte der Exponentialverteilung für ausgewählte $\lambda$

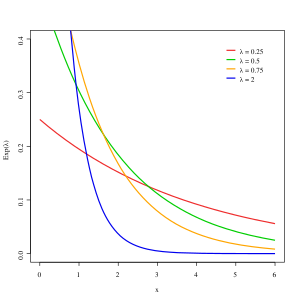
$Ex(\tau ),\tau >0$, kontinuierlich, asymmetrisch

$\tau$ ist der Erwartungswert. Manchmal wird die Exponentialverteilung auch durch die konstante Ausfallsrate $\lambda$ beschrieben. Im folgenden sind daher immer zwei Formen für die Exponentialverteilung angebeben. Die Dichtefunktion ist gegeben als:

$f(t)={\begin{cases}{\tfrac {1}{\tau }}e^{-{\frac {t}{\tau }}}&{\mbox{fuer }}t>0\\0&{\mbox{sonst}}\end{cases}}\qquad f(t)={\begin{cases}\lambda e^{-\lambda t}&{\mbox{fuer }}t>0\\0&{\mbox{sonst}}\end{cases}}$

Die Verteilungsfunktion ist gegeben als

$F(t)={\begin{cases}1-e^{-{\frac {t}{\tau }}}&{\mbox{fuer }}t>0\\0&{\mbox{sonst}}\end{cases}}\qquad F(t)={\begin{cases}1-e^{-\lambda t}&{\mbox{fuer }}t>0\\0&{\mbox{sonst}}\end{cases}}$

Der Erwartungswert ist dann

$E(T)=\tau \qquad E(T)={\frac {1}{\lambda }}$

und die Varianz ist

$Var(T)=\tau ^{2}\qquad Var(T)={\frac {1}{\lambda ^{2}}}$

Die Exponentialverteilung ist ein Modell fuer die zufaellige Dauer von Zeitintervallen. Eine wichtige Anwendung der Exponentialverteilung ist die Errechnung der "Mean Time Between Failure", also der durschnittlichen Lebenserwartung, von Bauteilen die keiner Alterung unterliegen.

Siehe auch die Exponentialverteilung auf der deutschen Wikipedia. Im Skriptum wird die Exponentialverteilung auch in Kapitel 9.3.1, S. 125 ff. behandelt.

Rechtecksverteilung

$R(a,b)$: stetig, symmetrisch.

Erwartungswert: ${\tfrac {1}{2}}(a+b)$, Varianz: ${\tfrac {1}{12}}(b-a)^{2}$

Lognormalverteilung

$X\approx N(\mu ,\sigma ^{2})$, $Y=e^{X}$. Y folgt Lognormalverteilung

Weitere Formeln

Formelsammlung aus dem Vowi