TU Wien:Analysis 2 UE (diverse)/Übungen SS23/Beispiel 39
Man bestimme alle relativen Extrema und Sattelpunkte der Funktion im Inneren des angegebenen Bereichs und alle absoluten Extrema im gesamten, angegebenen Bereich. Hinweis: Eine symmetrische 2x2-Matrix ist genau dann indefinit, wenn ihre Determinante negativ ist.
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Hilfreiches[Bearbeiten | Quelltext bearbeiten]
Kurvendiskussion[Bearbeiten | Quelltext bearbeiten]
Nullstellen:
Extremwerte:
- Maximum, falls
- Minimum, falls
- Sattelpunkt, falls
Wendepunkte:
und
Konvexität:
- Linkskrümmung/Konvexbogen (nach oben offen), falls
- Rechtskrümmung/Konkavbogen (nach unten offen), falls
In der Wikipedia findet sich dazu ein langer Artikel.
Für Funktionen in zwei Parametern gehen die Bedingungen aus hilfreichen PDF von Dr. Thomas Zehrt der Universität Basel auf Seite 6 hervor.
Für eine Maximalstelle muss demnach gelten: wobei und zusätzlich
Für eine Minimalstelle muss demnach gelten: wobei und zusätzlich
Für einen Sattelpunkt muss demnach gelten: wobei
Lösungsvorschlag von Usernamee[Bearbeiten | Quelltext bearbeiten]
--Usernamee 19:34, 24. Sep. 2021 (CEST)
Schritt eins: Ableiten in allen Formen und Farben[Bearbeiten | Quelltext bearbeiten]
(Produktregel beachten)
(Produktregel beachten)
Schritt zwei: Nullsetzen der Ableitung nach X[Bearbeiten | Quelltext bearbeiten]
Also ist die Ableitung nach X im Ursprung und am Einheitskreis null.
Schritt drei: Nullsetzen der Ableitung nach Y[Bearbeiten | Quelltext bearbeiten]
Scheint nicht so ganz jemals möglich zu sein.
Also ist die Ableitung nach Y bei null.
Schritt vier: Interessante Punkte analysieren[Bearbeiten | Quelltext bearbeiten]
Der Ursprung[Bearbeiten | Quelltext bearbeiten]
Bei gibt es also einen interessanten Punkt.
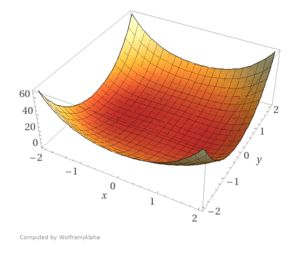
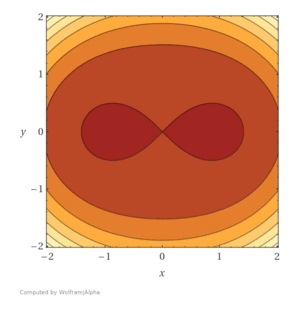
Es scheint ein Sattelpunkt zu sein. Sieht man sich nun die graphische Darstellung an, mag das auf den ersten Blick nicht auffallen. Das Bild der Höhenlinien hingegen zeigt sehr schön, dass es sich im Nullpunkt nicht um einen Tiefpunkt handelt.
Wenn y = 0 und der Einheitskreis sich schneiden[Bearbeiten | Quelltext bearbeiten]
Weitere Interessante Punkte gibt es nur am Schnitt von und dem aus ergehenden Einheitskreis. Also bei und .
Damit sind alle Bedingungen für eine Minimalstelle erfüllt.
Damit sind alle Bedingungen für eine Minimalstelle erfüllt.
Zusammenfassung[Bearbeiten | Quelltext bearbeiten]
Zusammenfassend kann man also sagen: Es gibt einen Sattelpunkt bei (0, 0) und Minima bei (-1, 0) und (1, 0).