Man bestimme die reelle und die komplexe Fourierreihe der 2 π {\displaystyle 2\pi }
f ( t ) = max { cos t , 0 } = 1 2 ( cos t + | cos t | ) {\displaystyle f(t)=\max \left\{\cos t,0\right\}={\frac {1}{2}}\left(\cos t+\left|\cos t\right|\right)}
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier:
Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
cos 2 x = 1 2 ( 1 + cos 2 x ) {\displaystyle \cos ^{2}x={\frac {1}{2}}\left(1+\cos 2x\right)}
cos x cos y = 1 2 ( cos ( x − y ) + cos ( x + y ) ) {\displaystyle \cos x\cos y={\frac {1}{2}}\left(\cos(x-y)+\cos(x+y)\right)}
c n = { ( a n + i b n ) 2 n < 0 a 0 2 n = 0 ( a n − i b n ) 2 n > 0 {\displaystyle c_{n}={\begin{cases}{\frac {(a_{n}+ib_{n})}{2}}&n<0\\{\frac {a_{0}}{2}}&n=0\\{\frac {(a_{n}-ib_{n})}{2}}&n>0\end{cases}}}
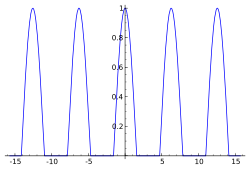
Plot von max { cos x , 0 } {\displaystyle \max \left\{\cos x,0\right\}} Da f {\displaystyle f} f ( − t ) = f ( t ) {\displaystyle f(-t)=f(t)}
∫ 0 2 π f ( t ) d t = 2 ∫ 0 π f ( t ) d t {\displaystyle \int _{0}^{2\pi }f(t)\mathrm {d} t=2\int _{0}^{\pi }f(t)\mathrm {d} t}
und die ihr zugeordnete Fourierreihe ist eine reine Cosinusreihe
f ^ ( t ) = a 0 2 + ∑ k = 1 ∞ a k cos k t {\displaystyle {\hat {f}}(t)={\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }a_{k}\cos kt}
mit
a k = 2 2 π ∫ 0 2 π f ( t ) ⋅ cos k t d t = 2 π ∫ 0 π f ( t ) ⋅ cos k t d t = 2 π ∫ 0 π max { cos t , 0 } ⋅ cos k t d t = 2 π ∫ 0 π 2 cos t ⋅ cos k t d t {\displaystyle {\begin{aligned}a_{k}&={\frac {2}{2\pi }}\int _{0}^{2\pi }f(t)\cdot \cos kt\,\mathrm {d} t\\&={\frac {2}{\pi }}\int _{0}^{\pi }f(t)\cdot \cos kt\,\mathrm {d} t\\&={\frac {2}{\pi }}\int _{0}^{\pi }\max \left\{\cos t,0\right\}\cdot \cos kt\,\mathrm {d} t\\&={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\cos t\cdot \cos kt\,\mathrm {d} t\end{aligned}}}
Daraus kann man nun die einzelnen Fourierkoeffizienten berechnen:
a 0 = 2 π ∫ 0 π 2 cos t ⋅ cos 0 t d t = 2 π ∫ 0 π 2 cos t ⋅ 1 d t = 2 π sin t | 0 π 2 = 2 π ( sin π 2 − sin 0 ) = 2 π ( 1 − 0 ) = 2 π {\displaystyle {\begin{aligned}a_{0}&={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\cos t\cdot \cos 0t\,\mathrm {d} t\\&={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\cos t\cdot 1\,\mathrm {d} t\\&={\frac {2}{\pi }}\left.\sin t\right|_{0}^{\frac {\pi }{2}}\\&={\frac {2}{\pi }}\left(\sin {\frac {\pi }{2}}-\sin 0\right)\\&={\frac {2}{\pi }}\left(1-0\right)\\&={\frac {2}{\pi }}\end{aligned}}}
a 1 = 2 π ∫ 0 π 2 cos t ⋅ cos 1 t d t = 2 π ∫ 0 π 2 cos 2 t d t = 2 π ∫ 0 π 2 1 2 ( 1 + cos 2 t ) d t = 1 π ∫ 0 π 2 1 + cos 2 t d t = 1 π ( t + 1 2 sin 2 t ) | 0 π 2 = 1 π ( π 2 + 1 2 sin 2 π 2 − 0 − 1 2 sin 0 ) = 1 π ( π 2 + 0 − 0 − 0 ) = 1 2 {\displaystyle {\begin{aligned}a_{1}&={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\cos t\cdot \cos 1t\,\mathrm {d} t\\&={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}\cos ^{2}t\,\mathrm {d} t\\&={\frac {2}{\pi }}\int _{0}^{\frac {\pi }{2}}{\frac {1}{2}}\left(1+\cos 2t\right)\,\mathrm {d} t\\&={\frac {1}{\pi }}\int _{0}^{\frac {\pi }{2}}1+\cos 2t\,\mathrm {d} t\\&={\frac {1}{\pi }}\left(\left.t+{\frac {1}{2}}\sin 2t\right)\right|_{0}^{\frac {\pi }{2}}\\&={\frac {1}{\pi }}\left({\frac {\pi }{2}}+{\frac {1}{2}}\sin 2{\frac {\pi }{2}}-0-{\frac {1}{2}}\sin 0\right)\\&={\frac {1}{\pi }}\left({\frac {\pi }{2}}+0-0-0\right)\\&={\frac {1}{2}}\end{aligned}}}
a 1 {\displaystyle a_{1}} a k {\displaystyle a_{k}}
a k = 2 π ∫ 0 π 2 cos t ⋅ cos k t d t = 2 π ∫ 0 π 2 1 2 ( cos ( k t − t ) + cos ( k t + t ) ) d t = 1 π ∫ 0 π 2 cos ( ( k − 1 ) t ) + cos ( ( k + 1 ) t ) d t = 1 π ( 1 k − 1 sin ( ( k − 1 ) t ) + 1 k + 1 sin ( ( k + 1 ) t ) ) | 0 π 2 = 1 π ( 1 k − 1 ( sin ( ( k − 1 ) π 2 ) − sin ( ( k − 1 ) 0 ) ) + 1 k + 1 ( sin ( ( k + 1 ) π 2 ) − sin ( ( k + 1 ) 0 ) )
Und als reelle Fourierreihe erhält man
f ^ ( t ) = a 0 2 + ∑ k = 1 ∞ a k cos k t = 1 π + 1 2 cos t + ∑ l = 1 ∞ 2 ( − 1 ) l π ( 1 − 4 l 2 ) cos 2 l t {\displaystyle {\begin{aligned}{\hat {f}}(t)&={\frac {a_{0}}{2}}+\sum _{k=1}^{\infty }a_{k}\cos kt\\&={\frac {1}{\pi }}+{\frac {1}{2}}\cos t+\sum _{l=1}^{\infty }{\frac {2(-1)^{l}}{\pi (1-4l^{2})}}\cos 2lt\end{aligned}}}
Für die komplexe Fourierreihe berechnet man einfach die komplexen Fourierkoeffizenten aus den reellen
c k = c − k = a k 2 = { 1 π k = 0 1 4 k ∈ { − 1 , 1 } 0 k ist ungerade ( − 1 ) k 2 π ( 1 − k 2 ) k ist gerade {\displaystyle c_{k}=c_{-k}={\frac {a_{k}}{2}}={\begin{cases}{\frac {1}{\pi }}&k=0\\{\frac {1}{4}}&k\in \{-1,1\}\\0&k{\text{ ist ungerade}}\\{\frac {(-1)^{\frac {k}{2}}}{\pi (1-k^{2})}}&k{\text{ ist gerade}}\end{cases}}}
und erhält somit als komplexe Fourierreihe
f ^ ( t ) = ∑ k = − ∞ ∞ c k e i k t = ∑ l = − ∞ − 1 ( − 1 ) l π ( 1 − 4 l 2 ) e 2 i l t + 1 4 e − i t + 1 π + 1 4 e i t + ∑ l = 1 ∞ ( − 1 ) l π ( 1 − 4 l 2 ) e 2 i l t = 1 π + 1 4 ( e i t + e − i t ) + ∑ l = 1 ∞ ( − 1 ) l π ( 1 − 4 l 2 ) ( e 2 i l t + e − 2 i l t ) {\displaystyle {\begin{aligned}{\hat {f}}(t)&=\sum _{k=-\infty }^{\infty }c_{k}e^{ikt}\\&=\sum _{l=-\infty }^{-1}{\frac {(-1)^{l}}{\pi (1-4l^{2})}}e^{2ilt}+{\frac {1}{4}}e^{-it}+{\frac {1}{\pi }}+{\frac {1}{4}}e^{it}+\sum _{l=1}^{\infty }{\frac {(-1)^{l}}{\pi (1-4l^{2})}}e^{2ilt}\\&={\frac {1}{\pi }}+{\frac {1}{4}}\left(e^{it}+e^{-it}\right)+\sum _{l=1}^{\infty }{\frac {(-1)^{l}}{\pi (1-4l^{2})}}\left(e^{2ilt}+e^{-2ilt}\right)\end{aligned}}}