TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 226

Angabe

Untersuchen Sie, ob die Menge M mit der Operation $\circ$ ein Gruppoid, eine Halbgruppe, ein Monoid bzw. eine Gruppe ist.

$M=𝔓(A)$, d.h. die Potenzmenge der Menge A, $B\circ C=B△C$ (die symmetrische Differenz)

Definition der symmetrischen Differenz

$A△B=(A\setminus B)\cup (B\setminus A)$

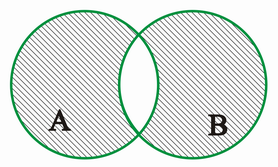
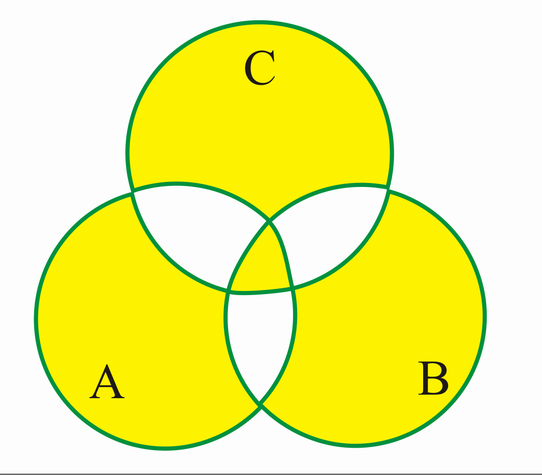
C heißt symmetrische Differenz der Mengen A und B,

$C=A\mathrm{△}B$,

wenn C alle Elemente aus A enthält, die nicht zu B gehören und alle Elemente aus B, die nicht zu A gehören, d.h.:

$A\mathrm{△}B=(A\mathrm{\setminus }B)\cup (B\mathrm{\setminus }A)=(A\cup B)\mathrm{\setminus }(A\cap B)$

VENN-Diagramm:

Theoretische Grundlagen (Zusammenfassung von mnemetz)

Gruppeneigenschaften

Gruppeneigenschaften

Gesetze und Eigenschaften von algebraischen Strukturen

Eine algebraische Struktur ist eine nichtleere Menge G mit einer oder mehreren Operationen.

Folgende Eigenschaften kann eine solche Struktur annehmen:

1. Abgeschlossenheit: für $a,b\in G$ ist $a\circ b\in G$ (d.h. ist eindeutig zugeordnet). Das $\circ$ entspricht einer Funktion $\circ :G\times G\to G$
2. Assoziativgesetz: $a\circ (b\circ c)=(a\circ b)\circ c$ für alle $a,b,c\in G$.
3. Einheitselement (bzw. Neutrales Element): Es existiert ein $e\in G$, so dass für alle $a\in G$ gilt: $a\circ e=e\circ a=a$.
4. Inverses Element: Für jedes $a\in G$ gibt es ein inverses Element $a^{\prime }\in G$ (oder auch $a^{-1}$) so, dass gilt $a\circ a^{\prime }=a^{\prime }\circ a=e$. Wobei das e das Einheitselement ist.
5. Kommutativgesetz: $a\circ b=b\circ a$ für alle $a,b\in G$.

Nr.	Gruppoid	Halbgruppe	Monoid	Gruppe	Abelsche Gruppe
1	✓	✓	✓	✓	✓
2		✓	✓	✓	✓
3			✓	✓	✓
4				✓	✓
5					✓

Lösungsvorschlag von mnemetz

Abgeschlossenheit

Wie schon aus den VENN-Diagrammen hervorgeht, ist eine Abgeschlossenheit gegeben.

Assoziativität

$(A\mathrm{△}B)\mathrm{△}C=A\mathrm{△}(B\mathrm{△}C)$

Es liegt die Assoziativität vor!

Man könnte dies mit der Elementtafel nachweisen (Auszug):

$A$	$B$	$C$	\	$A\mathrm{△}B$	$(A\mathrm{△}B)\mathrm{△}C$	\	$B\mathrm{△}C$	$A\mathrm{△}(B\mathrm{△}C)$
$\in$	$\in$	$\in$	\	$\notin$	$\in$	\	$\notin$	$\in$
$\in$	$\in$	$\notin$	\	$\notin$	$\notin$	\	$\in$	$\notin$

neutrales Element (Einheitselement)

Das neutrale Element existiert', es ist die leere Menge $\varnothing$, denn $A△\varnothing =\varnothing △A=A\mathrm{\forall }A\in 𝔓(M)$.

Inverses Element

Auch das inverse Element existiert, und zwar A' = A: jedes Element ist zu sich selbst invers denn $A△A^{\prime }=A^{\prime }△A=\varnothing \mathrm{\forall }A\in 𝔓(M)$

$\bar{A}$ ist im folgenden das Komplement von A

$A\mathrm{△}{A}^{\prime }=(A\cap \bar{A})\cup (\bar{A}\cap A)$

Beruhend auf dem Gesetzen von de Morgan und dem Distributivgesetz folgt dann: $A\cap \bar{A}=\bar{A}\cap A=\mathrm{\varnothing }$

Versuch einer Erklärung zu f.thread:37942 --Mnemetz 20:39, 12. Dez 2005 (CET)

Kommutativität

Auch eine Kommutativität liegt vor.

$𝔓(M):(A△B)=(A\mathrm{\setminus }B)\cup (B\mathrm{\setminus }A)=(A\cap B)\mathrm{\setminus }(A\cap B)$ - die symmetrische Differenz ist daher kommutativ

Schlussfolgerung

Es liegt ein Abelsche Gruppe vor.

Webressourcen

• http://de.wikipedia.org/wiki/Mengenlehre