TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 33

Man berechne rechnerisch (ohne Taschenrechner) alle Werte vom $\sqrt[5]{18-6\sqrt{3}i}$ in der Form $[r,\varphi ]$.

Umrechnung in die Polarform

Einleitende Berechnungen

Es gilt zur Umrechnung in die Polarform: $z=r\ast (\cos \varphi +i\ast \sin \varphi )$!

Die der umzurechnede Gleichung ist: $z^5=18-6\sqrt{3}i$

• $r=|z|=\sqrt{a^2+b^2}=\sqrt{18^2+36\ast 3}=\sqrt{18(18+2\ast 3)}=3\ast \sqrt{2(18+6)}=3\ast \sqrt{48}=3\ast \sqrt{4\ast 4\ast 3}=12\ast \sqrt{3}$
• $\varphi =arctan\frac{b}{a}$ da $a>0arctan\frac{6\ast \sqrt{3}}{18}=arctan\frac{\sqrt{3}}{3}=arctan\frac{\sqrt{3}}{\sqrt{3}\sqrt{3}}=arctan\frac{1}{\sqrt{3}}=30^{\circ }$

Ein zu führender Nachweis

Nachweis mittels gleichseitigem Dreieck

Wir müssen nun beweisen, dass $arctan-\frac{1}{\sqrt{3}}=30^{\circ }$ gilt.

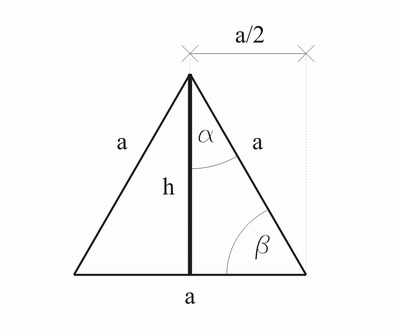
Man hat ein gleichseitiges Dreieck. Die Hälfte dieses Dreiecks ist ein rechtwinkeliges Dreieck, wobei die anderen beiden Winkel 60° und 30° haben.

Die Höhe des gleichseitigen Dreiecks ist: $h=\sqrt{a^2-{\frac{a}{2}}^2}$

Wir können das vereinfachen:

$h=\sqrt{a^2-(\frac{a}{2}{)}^2}=\sqrt{a^2\ast (1-\frac{1}{4})}=a\ast \sqrt{\frac{3}{4}}=\frac{a}{2}\ast \sqrt{3}$

Von nun an gehen wir vom halben Dreieck aus, wobei das alte h nun zu einer Kathete wird: $\tan \alpha =\frac{G}{A}\alpha$ ist der Winkel, der durch die Dreieckshalbierung in der Mitte durchgeschnitten wurde; G=Gegenkathete, A=Ankathete, der Winkel $\alpha$ ist 30°.

$\tan \alpha =\frac{0.5\ast a}{h}$

$\tan \alpha =\frac{0.5\ast a}{h}$

$\tan \alpha =\frac{\frac{0.5\ast a}{0.5\ast a}}{\sqrt{3}}$

$\tan \alpha =\frac{1}{\sqrt{3}}$

Also gilt umgekehrt: $arctan\frac{1}{\sqrt{3}}=30^{\circ }$ Q.e.d.

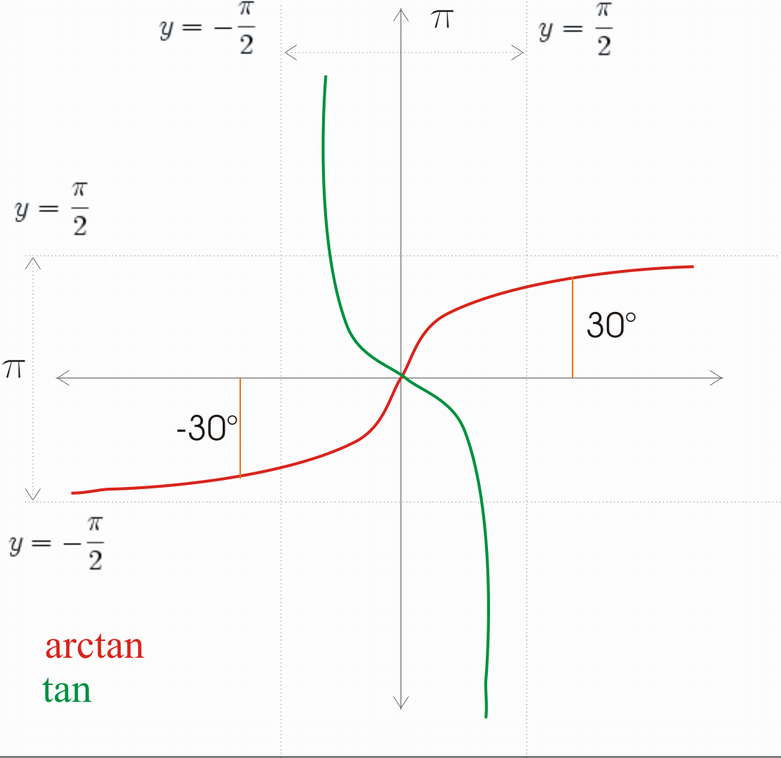
(arctan ist die Umkehrfunktion von tan!)

Unser Ergebnis oben vor dem Nachweis hat ein negatives Vorzeichen - aber bei der arctan-Funktion liefern 30° und -30° denselben Wert (betragsmässig):

Nachweis mittels Einheitskreis

Durch die Beziehungen

• $\cos \varphi =\frac{a}{r}=\mathrm{...}=\frac{1}{2\sqrt{3}}$
• $\sin \varphi =\frac{b}{r}=\mathrm{...}=-\frac{1}{2}$

kann unter Verwendung des Einheitskreises auch die Analogie -30° = $-\frac{\pi }{6}$ nachgewiesen werden.

Umrechnung in Polarkoordinaten

$arctan-\frac{1}{\sqrt{3}}=-30^{\circ }=-\frac{\pi }{6}$

(Folgendes bis zur Lösung sind nur Anmerkungen)!

Zuerst Angabe in Grad, danach in Bogenmaß. Die Umrechnungsformeln sind:

• Von Grad nach Bogenmaß:

${\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{k}\mathrm{e}\mathrm{l}}_{\mathrm{B}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}=\frac{{\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{k}\mathrm{e}\mathrm{l}}_{\mathrm{G}\mathrm{r}\mathrm{a}\mathrm{d}}\cdot \pi }{180}$

• Von Bogenmaß nach Grad:

${\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{k}\mathrm{e}\mathrm{l}}_{\mathrm{G}\mathrm{r}\mathrm{a}\mathrm{d}}=\frac{{\mathrm{W}\mathrm{i}\mathrm{n}\mathrm{k}\mathrm{e}\mathrm{l}}_{\mathrm{B}\mathrm{o}\mathrm{g}\mathrm{e}\mathrm{n}\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}\cdot 180}{\pi }$

Polarformdarstellung der Gleichung:

$z^5=12\ast \sqrt{3}\ast (\cos -\frac{\pi }{6}+i\ast \sin -\frac{\pi }{6})$

Lösung

Mittels Satz von Moivre

Die "Wurzelformel" ist: (Siehe auch https://web.archive.org/web/20180817161334/https://de.wikibooks.org/wiki/Komplexe_Zahlen/_Weitere_Rechenverfahren sowie das Beispiel danach auf dieser Website)

$z_{0,\mathrm{...},4}=\sqrt[5]{12\ast \sqrt{3}}\ast (\cos \frac{-\frac{\pi }{6}+k\ast 2\pi }{5}+i\sin \frac{-\frac{\pi }{6}+k\ast 2\pi }{5})k=\{0,1,2,3,4\}$

andere Form

$w=[\sqrt[n]{r};\frac{\varphi +2\pi k}{n}]n=5k=0,1,2,3,4$

Danksagung

Ich danke Christoph R. für den Hinweis und die Entschlüsselung von http://www.emath.de/Mathe-Board/messages/7/14736.html?1110537571 - siehe auch f.thread:36246 ! --Mnemetz 21:26, 6. Nov 2005 (CET)

Ressourcen

Andere Beispiele

Beispiele 28 bis 39

Vorlesung

• 4._VO_19.10.2005
• 5._VO_24.10.2005

Foren

• f.thread:36246

Websites

• Bogenmaß
• Eine Frage zu arctan
• Wikipedia-Eintrag Bogenmaß
• Umrechnung von Polarkoordinaten in kartesische Koordinaten