Untersuchen Sie, ob  Teilraum des Vektorraums
Teilraum des Vektorraums  über
über  ist und beschreiben Sie die Menge
ist und beschreiben Sie die Menge  geometrisch:
geometrisch:

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier:
Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
- Untervektorraum
Untervektorraum[Bearbeiten, Wikipedia, 3.05 Definition]
Sei  ein Vektorraum,
ein Vektorraum,  heißt Unterraum oder Teilraum, wenn:
heißt Unterraum oder Teilraum, wenn:

 ist abgeschlossen bezüglich
ist abgeschlossen bezüglich 
 ist abgeschlossen bezüglich
ist abgeschlossen bezüglich 
Kriterium 1 des Unterraumkriteriums,  , ist erfüllt, da es Vektoren gibt, für die gilt
, ist erfüllt, da es Vektoren gibt, für die gilt  , wie z. B.
, wie z. B.

Es gilt hier die Abgeschlossenheit bzgl. Addition von  zu prüfen.
zu prüfen.
Das zweite Kriterium ist nicht erfüllt, da nicht für jede Addition zweier Vektoren aus U gilt, dass die Summe wieder  erfüllt. Wir wählen z. B. die folgenden Vektoren und addieren:
erfüllt. Wir wählen z. B. die folgenden Vektoren und addieren:

Nun müsste für die Summe der beiden Vektoren gelten  . Dies ist jedoch nicht der Fall, weil
. Dies ist jedoch nicht der Fall, weil  : Keine Abgeschlossenheit bzgl. Addition lt. Kriterium 2.
: Keine Abgeschlossenheit bzgl. Addition lt. Kriterium 2.
Das dritte Kriterium ist auch nicht erfüllt, weil für jedes Produkt eines Vektors aus U mit einem Skalar  aus
aus  gelten müsste, dass es wieder die Kondition
gelten müsste, dass es wieder die Kondition  erfüllt (Abgeschlossenheit bzgl. Multiplikation von
erfüllt (Abgeschlossenheit bzgl. Multiplikation von  ). Dies ist jedoch auch nicht der Fall.
). Dies ist jedoch auch nicht der Fall.
z. B.

Diese Gleichung stimmt nur für  und nicht für alle Werte des Körpers
und nicht für alle Werte des Körpers  . Somit ist auch das dritte Kriterium nicht erfüllt. Es handelt sich bei W also nicht um einen Teilraum des oben genannten Vektorraums.
. Somit ist auch das dritte Kriterium nicht erfüllt. Es handelt sich bei W also nicht um einen Teilraum des oben genannten Vektorraums.
Shikantaza 19:24, 30. Mai 2009 (CEST)
- Vektorraum
Vektorraum[Bearbeiten, Wikipedia, 3.02 Definition]
Sei  eine abelsche Gruppe und
eine abelsche Gruppe und  ein Körper.
ein Körper.  heißt Vektorraum, wenn
heißt Vektorraum, wenn
 folgendes gilt:
folgendes gilt:




Sei  ein Vektorraum,
ein Vektorraum,  heißt Unterraum oder Teilraum, wenn:
heißt Unterraum oder Teilraum, wenn:

 ist abgeschlossen bezüglich
ist abgeschlossen bezüglich 
 ist abgeschlossen bezüglich
ist abgeschlossen bezüglich 
--Har203 20:57, 2. Mär. 2026 (CET)
Untersuchen Sie, ob  Teilraum des Vektorraums
Teilraum des Vektorraums  über
über  ist und beschreiben Sie die Menge
ist und beschreiben Sie die Menge  geometrisch:
geometrisch:

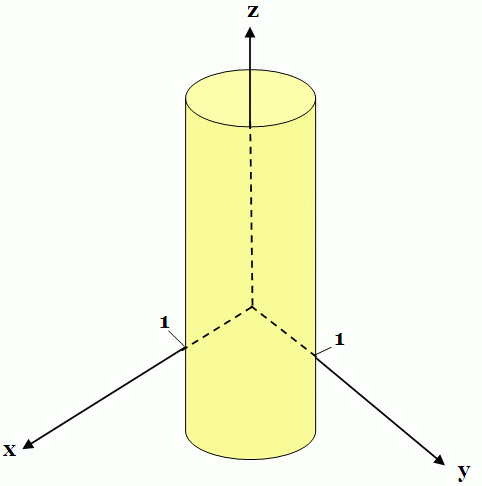
Anmerkung:  . D.h. in der
. D.h. in der  -Ebene handelt es sich um einen Kreis, um den Einheitskreis in der Ebene. Da
-Ebene handelt es sich um einen Kreis, um den Einheitskreis in der Ebene. Da  beliebig ist, entsteht ein leeres Rohr mit dem Radius
beliebig ist, entsteht ein leeres Rohr mit dem Radius  , welches genau um die
, welches genau um die  -Achse als Mittelpunkt entsteht.
-Achse als Mittelpunkt entsteht.
Anmerkung: Der kürzeste Gegenbeweis ist wohl:  ist kein Untervektorraum von
ist kein Untervektorraum von  .
.
Nicht leer:
 , da
, da  mit
mit  .
.
Abgeschlossen bezüglich Addition:
- Seien
 mit
mit

 müsste den Wert
müsste den Wert  annehmen:
annehmen:- Gegenbeispiel:
 beide
beide  und für die Summe gilt
und für die Summe gilt  .
.
- Daher ist
 bezüglich der Addition
bezüglich der Addition  abgeschlossen.
abgeschlossen.
Abgeschlossen bezüglich der Skalarmultiplikation:
- Seien
 .
.
 mit
mit  .
.
- Gegenbeispiel:
 . Weiters sei
. Weiters sei  .
.
 .
.
- Daher ist
 bezüglich der Skalarmultiplikation ebenfalls
bezüglich der Skalarmultiplikation ebenfalls  abgeschlossen.
abgeschlossen.
Geometrische Interpretation:  ist in der Ebene bekanntlich ein Kreis mit dem Radius
ist in der Ebene bekanntlich ein Kreis mit dem Radius  . Im Raum ist
. Im Raum ist  ein Kreis in der
ein Kreis in der  -Ebene. Da der Radius
-Ebene. Da der Radius  ist, beschreibt diese vorab einmal den Einheitskreis (ohne Berücksichtigung der
ist, beschreibt diese vorab einmal den Einheitskreis (ohne Berücksichtigung der  -Achse). Weiters ist die
-Achse). Weiters ist die  -Koordinate
-Koordinate  beliebig, also wird aus dem Kreis ein Hohlzylinder, mit einem Radius von
beliebig, also wird aus dem Kreis ein Hohlzylinder, mit einem Radius von  und dem Mittelpunkt des Zylinders der
und dem Mittelpunkt des Zylinders der  -Achse.
-Achse.
Gesamtergebnis:  .
.  ist
ist  Unterraum des
Unterraum des  über
über  . Die Menge
. Die Menge  ist zwar nicht leer (
ist zwar nicht leer ( ), aber weder die Addition, noch die Skalarmultiplikation sind abgeschlossen.
), aber weder die Addition, noch die Skalarmultiplikation sind abgeschlossen.  .
.
Wikipedia:
Ähnliche Beispiele:
Weitere Beispiele:
