TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 129

Welche der Eigenschaften Reflexivität, Symmetrie, Antisymmetrie und Transitivität hat die folgende Relation R auf $\mathbb {Z}$ :
m R n $\Leftrightarrow m^{2}=n^{2}$

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Hilfreiches[Bearbeiten | Quelltext bearbeiten]

Reflexivität

Reflexivität

$\forall a\in M:\quad aRa$

Symmetrie

Symmetrie

$\forall a,b\in M:aRb\Rightarrow bRa$

Antisymmetrie

Antisymmetrie

$\forall a,b\in M:\quad aRb\wedge bRa\Longrightarrow a=b$

Transitivität

Transitivität

$\forall a,b,c\in M:\quad a\circ b\wedge b\circ c\Rightarrow a\circ c$

Vorüberlegungen[Bearbeiten | Quelltext bearbeiten]

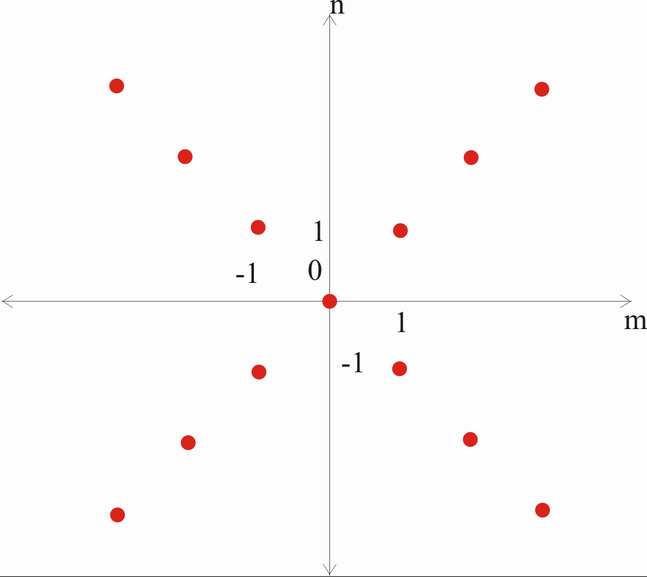
Zuerst mal eine kleine Skizze:

Hilfreich ist es auch, mal einen kleinen Teil der Lösungsmenge aufzuschreiben:

L = { ... (-2,-2), (-2,2), (2,-2), (-1,-1), (-1,1), (1,-1), (0,0), (1,1), (2,2) ... }

Reflexivität[Bearbeiten | Quelltext bearbeiten]

Reflexivität heißt, dass jedes Element in Relation zu sich selbst steht:

$\forall {\text{ a }}\in {\text{ A }}:{\text{ (a,a) }}\in {\text{ R }}$

Ja, da m = n und ${\text{L }}\forall {\text{ ( m = n ) }}=$ {... (-2,-2), (-1,-1), (0,0), (1,1), (2,2) ...}.

Symmetrie[Bearbeiten | Quelltext bearbeiten]

Symmetrie heißt, wenn für alle a,b mit aRb auch bRa folgt.

$\forall {\text{ a,b }}\in {\text{ }}A^{2}:{\text{ (a,b) }}\in {\text{ R }}\qquad \Rightarrow \qquad {\text{ (b,a) }}\in {\text{ R }}$

Ja, trifft zu.

Antisymmetrie[Bearbeiten | Quelltext bearbeiten]

R heisst anti-symmetrisch wenn aus aRb und bRa stets a=b folgt.

Nein, das trifft nicht zu.

Erklärung:

Es gibt auch unterschiedliche Werte bei denen die Relation gilt, zB $2^{2}=(-2)^{2}$ und $(-2)^{2}=2^{2}$

Bei der Antisymetrie müssten es jedoch die selben sein.

Transitivität[Bearbeiten | Quelltext bearbeiten]

Eine Relation R transitiv, wenn gilt: (a,b) aus R UND (b,c) aus R FOLGT (a,c) aus R

$\forall {\text{ a,b }}\in {\text{ R }}:{\text{ (a,b) }}\in {\text{ R }}\wedge {\text{ (b,c) }}\in {\text{ R }}\qquad \Rightarrow \qquad {\text{ (a,c) }}\in {\text{ R }}$

Untersuchen wir:

   a    b   ||   b   c   ||    a    c
  -1   -1   ||  -1  -1   ||   -1     -1    Erfüllt!!!
   1    1   ||   1   1   ||    1      1    Erfüllt!!!
   4    4   ||   4   4   ||    4      4    Erfüllt!!!

Somit liegt eine Transitivität vor! Und somit sind alle Bedingungen für eine Äquivalenzrelation erfüllt.