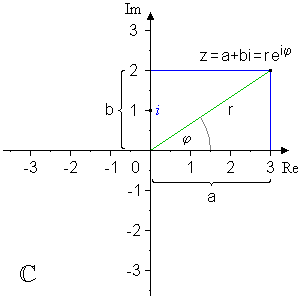TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 65

(Am 10.11. gründlich überarbeitet - sollte eigentlich so eine "Referatsvorlage" sein) :-) --Mnemetz 13:04, 10. Nov 2005 (CET)

Stellen Sie alle Lösungen der quadratischen Gleichung $z^{2}+4z+8=0$ sowohl in der Form $a+bi,a\in \mathbb {R}$ als auch in der Polarkoordinatenform $r*(cos\phi +i*sin\phi ),r\geq 0,0\leq \phi \leq 2\pi$ dar!

$z^{2}+4z+8=0$

Fundamentalsatz der Algebra

Gemäß dem Fundamentalsatz der Algebra hat eine Gleichung n-ten Grades mit Koeeffizienten in $\mathbb {C}$ n verschiedene Lösungen in $\mathbb {C}$ .

Unsere gegebene Gleichung ist zweiten Grades, daher sind zwei Lösungen zu erwarten.

Isolierung der Koeffizienten

Die gegebene quadratische Gleichung

$z^{2}+4z+8=0$

stellen wir allgemeiner wie folgt dar:

$az^{2}+bz+c=0$

a,b,c sind die Koeffizienten, und zwar:

a=1
b=4
c=8

Lösungen errechnen

Allgemeine Lösungsformel f. quadratische Gleichungen

$z_{1,2}={\frac {-b\pm {\sqrt {(b^{2}-4ac)}}}{2a}}$

Betrachtung der Diskriminante

Die Diskriminante (D) ist $b^{2}-4ac$ . Je nach Wert dr Diskriminante kann man feststellen, wieviele Lösungen es gibt sowie ob sie in $\mathbb {R}$ oder $\mathbb {C}$ zu erwarten sind.

Wenn gilt:

D > 0 $\Rightarrow$ verschiedene reelle Lösungen
D = 0 $\Rightarrow$ genau eine Lösung
D < 0 $\Rightarrow$ keine reelle Lösung

Unsere Diskriminante beträgt -16, daher werden wir zwei komplexe Lösungen erwarten!

Berechnung der Lösung

$z_{1,2}=-2\pm i{\sqrt {4}}=-2\pm 2i$

Umrechnung in die Polarform

Die Polarform ist definiert durch: $z=r*(\cos \phi +i*\sin \phi )$

Zuordnung der einzelnen Bestandteile:

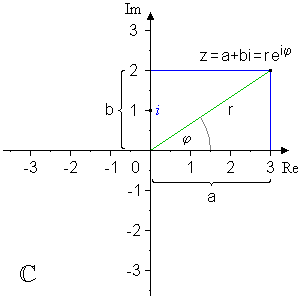Wobei

Berechnung von r

r ist der Betrag von z und ergibt sich aus der Formel $a^{2}+b^{2}=c^{2}$ für rechtwinkelige Dreiecke
$r=|z|={\sqrt {a^{2}+b^{2}}}={\sqrt {8}}$

Berechnung der Winkel

Berechnung von $\phi _{1}$ und $\phi _{2}$

Zur Orientierung und Vermeidung einer falschen Winkelannahme empfiehlt es sich, eine Skizze anzufertigen, aus der man in etwa die Lösungen entnehmen kann:

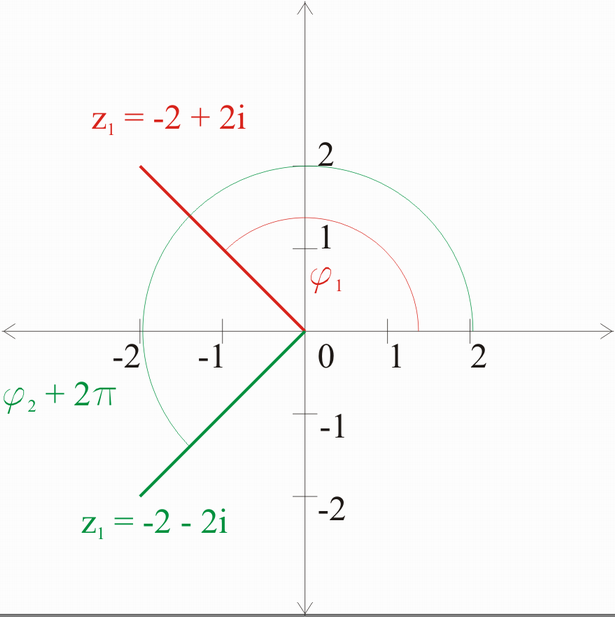
Allein schon diese Skizze sollte eventuelle irrige Winkelannahmen verhüten (z.B. 45°).

Regeln für arctan:

\varphi ={\begin{cases}\arctan {\frac {b}{a}}&\mathrm {f{\ddot {u}}r} \ a>0\\\arctan {\frac {b}{a}}+\pi &\mathrm {f{\ddot {u}}r} \ a<0,b\geq 0\\\arctan {\frac {b}{a}}-\pi &\mathrm {f{\ddot {u}}r} \ a<0,b<0\\\pi /2&\mathrm {f{\ddot {u}}r} \ a=0,b>0\\-\pi /2&\mathrm {f{\ddot {u}}r} \ a=0,b<0\end{cases}}

{}={\begin{cases}\arccos {\frac {a}{r}}&\mathrm {f{\ddot {u}}r} \ b\geq 0\\\arccos \left(-{\frac {a}{r}}\right)-\pi &\mathrm {f{\ddot {u}}r} \ b<0\end{cases}}

Unser a ist -2, also kleiner als Null. b kann zwei Werte annehmen, 2 oder -2 - daher müssen wir folgende Regeln anwenden:

$\phi _{1}$ $\phi _{1}$ bezieht sich auf $z_{1}=-2+2i$ $z_{1}=-2+2i$
- Zu berücksichtigen ist also die Regel für a < 0, b $\geq$ 0
- $\arctan {\frac {-2}{2}}+\pi =-45^{\circ }+180^{\circ }=135^{\circ }$
- $\pi$ entspricht 180°, $2*\pi$ entsprechen 360°
$\phi _{2}$ $\phi _{2}$ bezieht sich auf $z_{2}=-2-2i$ $z_{2}=-2-2i$
- Zu berücksichtigen ist also die Regel für a < 0, b $\leq$ 0
- $\arctan {\frac {-2}{-2}}-\pi =45^{\circ }-180^{\circ }=-135^{\circ }$

Somit erhalten wir die zwei Lösungen in der Polarform:

$z_{1}=r*(\cos \phi _{1}+i*\sin \phi _{1})={\sqrt {8}}*(cos(135^{\circ })+i*sin(135^{\circ }))\qquad \Rightarrow \qquad [{\sqrt {8}},135^{\circ }]\Rightarrow \qquad [{\sqrt {8}},{\frac {3}{4}}\pi ]$

$z_{2}=r*(\cos \phi _{2}+i*\sin \phi _{2})={\sqrt {8}}*(cos(-135^{\circ })+i*sin(-135^{\circ }))\qquad \Rightarrow \qquad [{\sqrt {8}},-135^{\circ }]\Rightarrow \qquad [{\sqrt {8}},-{\frac {3}{4}}\pi ]$

Und da ich bei $z_{2}{\text{ }}2\pi$ dazu addieren kann (entspricht 360°) erhalte ich als Winkel 225° und $[{\sqrt {8}},{\frac {5}{4}}\pi ]$

Zuerst wurden die Polarkoordinaten in Grad angegeben, danach in Bogenmaß. Die Umrechnungsformeln sind:

Von Grad nach Bogenmaß:

{\rm {Winkel}}_{\rm {Bogenmass}}={\frac {{\rm {Winkel}}_{\rm {Grad}}\cdot \pi }{180}}

Von Bogenmaß nach Grad:

{\rm {Winkel}}_{\rm {Grad}}={\frac {{\rm {Winkel}}_{\rm {Bogenmass}}\cdot 180}{\pi }}

Ressourcen

Andere Beispiele

Vorlesung

Foren

f.thread:36090

Websites